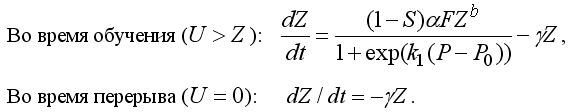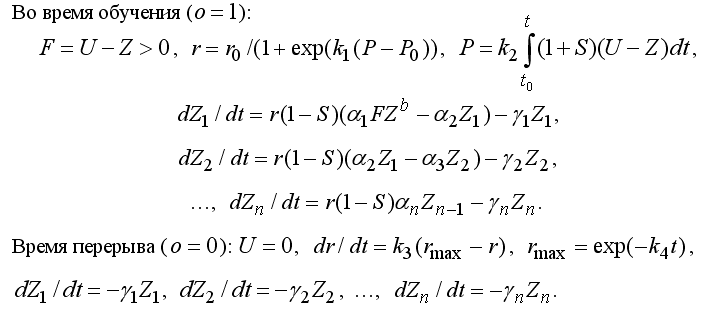Одна из важных проблем кибернетической педагогики состоит в следующем: как, зная параметры ученика, его исходный уровень знаний и воздействие, оказываемое учителем, предсказать знания ученика в последующие моменты времени. Метод имитационного моделирования позволяет создать компьютерную программу, симулирующую поведение системы “учитель–ученик” и исследовать влияние ее параметров на результат обучения.
Допустим, имеется учеников, каждый из которых характеризуется набором параметров a_i, b_i, g_i … (i =1, 2, …, n) и m учителей, владеющих методами M_1, M_2, M_3 и т.д. Основная задача дидактики состоит в том, чтобы так организовать учебный процесс, то есть выбрать методы и распределить изучаемый материал в течение заданного промежутка времени, чтобы в конце обучения учащиеся справились с системой тестов T = {T_1, T_2, …}. Обозначим через U уровень требований учителя. Сформулируем закон дидактики: скорость увеличения знаний Z пропорциональна прилагаемым усилиям F(t) ученика, эффективности методики обучения k, коэффициентам усвоения a и понимания П: dZ/dt = aПkF(t). Можно считать, что прилагаемые усилия ученика F пропорциональны разности между уровнем требований, предъявляемыми учителем и знаниями учащихся U – Z.
Рассмотрим частицу A массой m, прикрепленную к пружинке жесткостью k, которую за другой конец B тянут вдоль оси Ox. Координата точки B соответствует требованиям учителя U, а координата точки А –– количеству знаний Z учащегося. Действующая на частицу сила F пропорциональна разности U – Z и всегда направлена вдоль оси Ox. Она соответствует интенсивности воздействия учителя на ученика и пропорциональна мотивации ученика, его волевым усилиям. Тогда скорость перемещения частицы dv/dt = kF(t), что и соответствует сформулированному выше закону дидактики.
Усилия F, прилагаемые учащимся, характеризуют интенсивность его мыслительной деятельности и пропорциональны его мотивации M. Именно противоречие между требуемым и имеющимся уровнями знаний учащегося является движущей силой его учебной деятельности. Чем больше учащийся знает, тем легче он устанавливает ассоциативные связи и быстрее усваивает новые знания. Мотивация M к обучению зависит от воздействия учителя, то есть его уровня U требований учителя (количества знаний, которые необходимо усвоить), а также уровня знаний Z ученика. Не будем различать внешнюю мотивацию, обусловленную требованиями учителя, и внутреннюю мотивацию, вызванную собственным желанием ученика освоить соответствующую дисциплину. Чем больше M (а значит F) и знания Z учащегося, тем легче он устанавливает ассоциативные связи и быстрее усваивает новые знания. Психологи установили, что если уровень предъявляемых требований невысок, то мотивация к обучению отсутствует. Если уровень требований слишком высок и превышает некоторое критическое значение C, то мотивация также снижается. В идеале учитель должен правильно оценить состояние ученика и предъявлять ему такие требования, при которых его мотивация максимальна. Такой режим обучения, при котором требования U оптимальным образом согласуются с уровнем знаний Z данного ученика, и его мотивация максимальна, будем называть согласованным.
Создадим имитационную модель процесса обучения [1 – 8]. Скорость увеличения знаний ученика пропорциональна его коэффициенту научения a, работоспособности r, приложенным усилиям F и уровню знаний Z в степени b (b лежит в интервале от 0 до 1): dZ/dt = raFZ^b – gZ, где r –– коэффициент работоспособности, зависящий от степени усталости ученика, и g –– коэффициент забывания. Величина r по мере совершения учеником работы P сначала равна r_0 (r_0 лежит в интервале от 0 до 1), а затем плавно падает до 0 по закону: r = r_0/(1 + exp(k_1(P – P_0)). Здесь P_0 –– работа, совершаемая учеником (решение задач, выполнение заданий), при которой его работоспособность уменьшается от r_0 = 1 до r = 5. При обучении уровень требований учителя больше уровня знаний ученика (U > Z), и учебная работа, совершенная учеником (число выполненных заданий), зависит от приложенных усилий (интенсивности мыслительной деятельности) и длительности обучения. Усилия ученика F_i в течение dt_i пропорциональны его мотивации или разности между уровнем U_i предъявляемых требований и количеством знаний Z_i:
Если уровень предъявляемых требований мал (U не превышает Z), то есть ученик на уроке занят решением простых для него задач, то затрачиваемые им усилия пропорциональны времени: P = kt. Это позволяет учесть появление у ученика усталости и снижение работоспособности даже в случае, когда он выполняет простые задания длительное время. В перерывах между занятиями ученики отдыхают, их работоспособность восстанавливается по экспоненциальному закону:
где r_0 = r(t_0) –– работоспособность в момент начала отдыха t_0, где r_max –– максимальная работоспособность ученика в данное время t учебного дня. Она плавно снижается по закону r_max = exp(–k_4t). Скорость увеличения знаний при прочих равных условиях тем выше, чем меньше субъективная сложность (трудность понимания) S изучаемого материала: dZ/dt = r(1-S)aFZ^b – gZ. Сложность учебного материала S лежит в интервале от 0 до 1 и в общем случае зависит от уровня изучения других вопросов. Итак, получается модель:
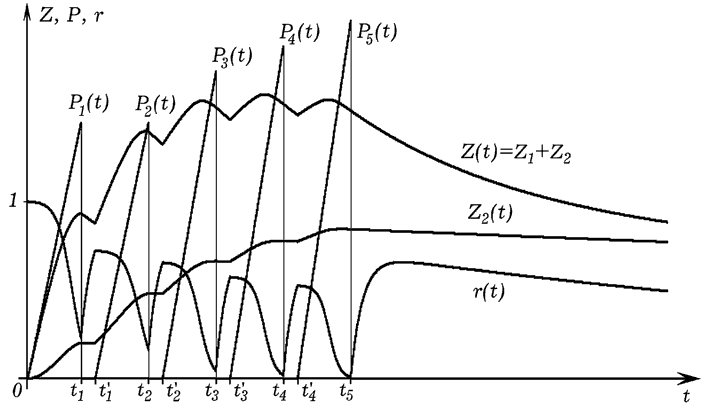
Допустим, учитель так организует процесс обучения в течение дня, что ученики работают с максимальным напряжением F = const. Прирост знаний существенно меньше общего количества знаний ученика Z, поэтому b = 0. Проводится 5 уроков одинаковой длительности T_u = t_1 = t_2 – t’_1 = … = t_5 – t’_4, разделенных перерывами длительностью T_p = t’_1 – t_1 = t’_2 – t_2 = … = t’_4 – t_4. Результаты имитационного моделирования –– на рис. 1. Параметры модели подобраны так, чтобы ее поведение соответствовало реальной ситуации. В интервале от 0 до t_5 коэффициент работоспособности r совершает колебания относительно плавно уменьшающегося значения. При уменьшении длительности перерывов между занятиями, учащиеся не успевают восстановить свою работоспособность, поэтому результаты обучения снижаются.
- Рис. 1. Результаты имитационного моделирования.
Усложним модель. При запоминании информации устанавливаются ассоциативные связи между новыми и имеющимися знаниями. В результате приобретенные знания становятся более прочными и забываются значительно медленнее. Пусть Z –– суммарные знания ученика, Z_1 –– самые “непрочные” знания первой категории с высоким коэффициентом забывания g_1, Z_2 –– знания второй категории с меньшим коэффициентом забывания g_2, …, а Z_n –– самые “прочные” знания n–ой категории с низким g_n (g_1 > g_2 > … > g_n). Коэффициенты усвоения a_i характеризуют быстроту перехода знаний (i – 1)–ой категории в более прочные знания i–ой категории. Пока происходит обучение, o = 1, а когда оно прекращается, o = 0. Коэффициент забывания g = 1 / T, где T –– время, уменьшения знаний в e = 2,72… раза. Обучение характеризуется не только количеством приобретенных знаний Z = Z_1 + Z_2 + … + Z_n, но и коэффициентом “прочности” Pr = (Z_2/2^(n – 2) + … + Z_(n – 1)/2 + Z_n)/Z.
При изучении одной темы сначала растет уровень знаний Z, затем происходит увеличение доли прочных знаний Z_n и повышается прочность Pr. Автором предложена обобщенная модель обучения, не имеющая аналогов в известной ему литературе. Пусть начальная работоспособность ученика r_0=1. В любой момент времени Z = Z_1(t) + Z_2(t) + … + Z_n(t).
Рис 2. Результаты моделирования (двухкопонентная модель).
Результаты моделирования –– на рис. 2 (программа ПР–1). Прочные знания в процессе обучения растут, а после не забываются. Другие модели обучения можно найти на сайте rmajer.narod.ru (komp-model.narod.ru).
Библиографический список
- Аткинсон Р., Бауэр Г., Кротерс Э. Введение в математическую теорию обучения. –– М: Мир, 1969. –– 486 с.
- Леонтьев Л.П., Гохман О.Г. Проблемы управления учебным процессом: Математические модели. –– Рига, 1984. –– 239 с.
- Майер Р.В. Исследование процесса формирования эмпирических знаний по физике. –– Глазов, ГГПИ: 1998. –– 132 c. (http://rmajer.narod.ru)
- Майер Р.В. Кибернетическая модель “учитель–ученик” // Домашняя лаборатория. Интернет-журнал. –– 2012. –– N 10. –– С. 333–340.
- Майер Р.В. Психология обучения без огорчения. Книга для начинающего учителя. –– Глазов: ГГПИ, 2010. –– 116 с.
- Новиков Д.А. Закономерности итеративного научения. –– М.: ИПУ, 1998. –– 77 с.
- Плотинский Ю.М. Модели социальных процессов: Учебное пособие для высших учебных заведений. –– M.: Логос, 2001. – 296 с.
- Шеннон Р. Имитационное моделирование систем: искусство и наука. –– М.: Мир, 1978. –– 302 с.