1. Введение.
Метод имитационного моделирования является одним из современных методов исследования процесса обучения [1, 8]. Он состоит в построении сначала математической, а затем компьютерной модели дидактической системы, и проведении с ней серии вычислительных экспериментов при различных условиях с целью установления или обоснования закономерностей [2–6]. Преимущество использования имитационных моделей при анализе системы “учитель–ученик” заключается в исчерпывающем перечислении и учете всех факторов, влияющих на ее поведение. Результаты компьютерных имитаций процесса обучения дополняют качественные рассуждения, повышают их объективность и обоснованность. Этот метод целесообразно использовать, если проведение педагогического эксперимента может дать отрицательный результат или сопряжено с большими затратами. Определенный интерес представляет решение оптимизационной задачи, заключающейся в поиске наиболее эффективного пути изучения некоторой дисциплины при наложенных ограничениях [4, 5, 7].
Рассмотрим урок, на котором учитель сначала объясняет новый материал, а затем учащиеся решают задачи или выполняют последовательность упражнений в заданном порядке. Если какой–либо ученик первым решил очередную задачу, то он выходит к доске и демонстрирует свое решение. Остальные ученики, глядя на решение, представленное на доске, тоже пытаются решить свою задачу. После того, как решена j–ая задача ученик переходит к решению (j+1)–ой задачи и т.д. Решив все m задач, ученик сдает тетрадь и выходит из класса.
Для моделирования этой ситуации используем мультиагентный подход. Он состоит в том, что все ученики имитируются независимыми агентами, функционирующими в виртуальном мире, состояние которого является результатом их взаимодействия. При этом они действуют автономно, у каждого из них нет информации о всей системе; агенты, полностью управляющие всей системой, отсутствуют. В некоторых компьютерных моделях используются программные агенты–автоматы, функционирующие в соответствии с заданным алгоритмом. В общем случае агенты могут обмениваться информацией друг с другом, получать информацию об окружающей среде и имеют возможность изменять ее состояние. Учтем, что каждый ученик характеризуется своим коэффициентом усвоения a_i и скоростью мышления v_i, равной числу совершаемых интеллектуальных действий в единицу времени. Чтобы получить статистически значимые результаты для данного набора учеников, проведем серию из 200 испытаний, в ходе которых определим среднее время T_i, затрачиваемое i–тым учеником для решения всех задач, и среднее число R_i самостоятельно решенных задач с демонстрацией их решения у доски.
2. Создание компьютерной модели.
В начале занятия n учеников изучают новую тему, а затем одновременно получают список из m=5–10 задач, которые они должны решить в заданном порядке. Чтобы решить каждую задачу, необходимо последовательно выполнить 10 операций (математических или других). Операции не повторяются, их общее количество M = 10 m. Если i–ый ученик правильно выполнил первые десять операций (O_i = 10), то он решил первую задачу, и переменной Z_i присваивается 1. При правильном выполнении 20 операций (O_i = 20) считается, что он решил первую и вторую задачи, Z_i равно 2. Если ученик выполнил первые 10S операций (O_i = 10S), то он решил первую вторую , …, S–тую задачи, Z_i присваивается S.
Выполнение действий –– вероятностный процесс. Ученик с номером i с вероятностью p_ij правильно выполняет операцию O_i = j и переходит к следующей операции, а с вероятностью (1 – p_ij) делает ошибку и снова пытается выполнить j–ую операцию (i = 1, 2, …, N; j = 1, 2, …, M). В начале занятия ученики не обучены, поэтому все p_ij равны 0,01. После обучения все p_ij увеличиваются на a_i*(1 – p_ij)*dt. Если ученик с номером i’ первым правильно решил задачу S, то он становится лидером ( L:= i ), идет к доске и в течение времени T_D демонстрирует свое решение всему классу, обучая остальных учеников. При этом переменной f[S] присваивается 1, счетчик самостоятельно решенных задач SR[i] увеличивается на 1, в результате обучения повышаются вероятности правильного выполнения операций p_ij для всех i и для j из интервала 10*(S–1)+1 до 10*S+1, которые соответствуют данной задаче. С каждым шагом по времени dt = 1 эти вероятности возрастают по закону p_ij := p_ij+a_i*(1–p_ij)*dt, где j = (10(S–1)+1), …, (10S+1). Показав свое решение на доске, лидер переходит к решению (S+1)–ой задачи. Остальные учащиеся, закончив задачу S, также переходят к следующей (S+1)–ой задаче. Ученик, решивший ее первым, становится лидером, и т.д.
Используется программа 1. На экране строится график зависимости номера выполненной операции O_i(t) и номера решенной задачи Z_i(t) для каждого ученика от времени. В силу случайных причин результаты реализаций исследуемого процесса отличаются друг от друга. Для получения статистически значимых результатов проводят серию из K_isp = 200 испытаний и для каждого ученика подсчитывают общее число самостоятельно решенных задач и общее время, затраченное на их решение (переменные SR[i], TR[i]). Необходимо отключить графический режим и, активизировав операторы writeln(…), вывести на экран TR[i] / K_isp и SR[i] / K_isp.
3. Результаты моделирования.
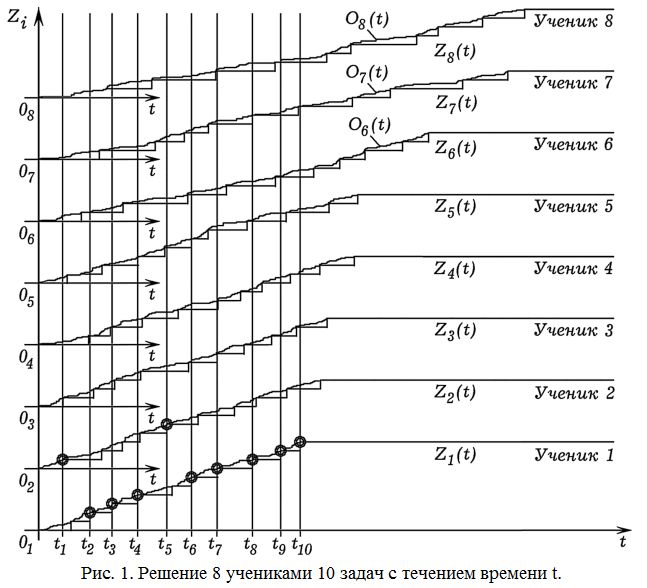
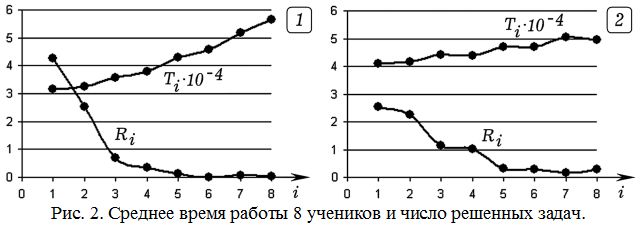
Результаты моделирования однократного решения группой из 8 учеников последовательности из 10 задач (зависимости O_i(t) и Z_i(t)) представлены на рис. 1 и 3. Кружками отмечается ученик, первым решивший очередную задачу, общее число кружков равно 10. Моменты времени, соответствующие этим событиям, отмечены вертикальными линиями. Рис. 1 соответствует ситуации, когда в классе находятся 8 учеников с коэффициентами усвоения a_i = (0,16, 0,15, 0,14, 0,12, 0,11, 0,10, 0,09, 0,08) и скоростью мышления (быстротой выполнения интеллектуальных действий) v_i = 1/d_i, где d_i = (9, 9, 10, 10, 11, 11, 12, 12), i = 1, 2, …, 8. Видно, что в данной реализации моделируемого процесса ученик 1 с самыми высокими коэффициентом усвоения и скоростью мышления первым решил 8 задач и раньше всех закончил работу, ученик 2 –– 2 задачи, остальные ученики не решили первыми ни одной задачи и закончили работу существенно позже. Так ученику 8 на решение всех задач потребовалось в 1,9 раза больше времени, чем ученику 1. При проведении серии из K_isp = 200 испытаний получаются следующие результаты (рис. 2.1). Ученик 1 затратил T_1= 31500 УЕВ (усл. ед. времени) и в среднем первым решил R_1= 4,3 задачи из 10, ученик 8 затратил T_8 = 56400 УЕВ и у доски решил в среднем R_8 = 0,02 из 10.
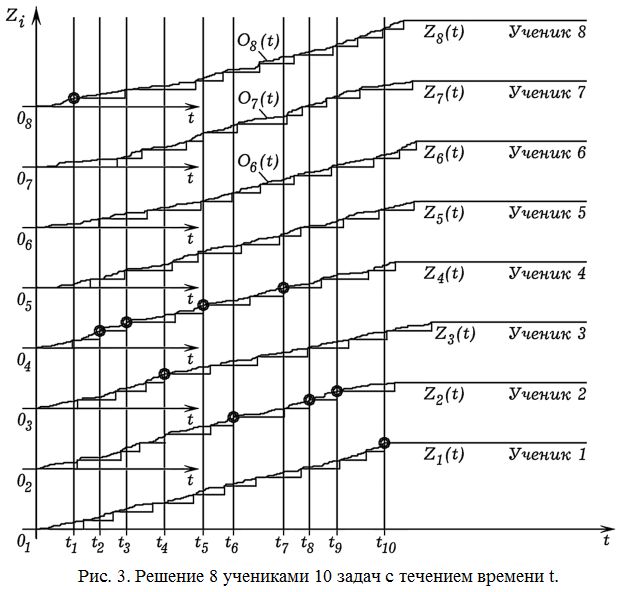
На рис. 3 представлены результаты имитационного моделирования решения задач учениками с одинаковыми коэффициентами усвоения a_i = 0,1 и различной скоростью мышления v_i = 1/d_i, где d_i = (9, 9, 10, 10, 11, 11, 12, 12), i = 1, 2, …, 8. Видно, что в данной реализации моделируемого процесса на выполнение задания ученикам потребовалось примерно одинаковое время, причем ученик 1, ученик 3 и ученик 8 первыми решили по 1 задаче, ученик 2 –– 3 задачи, ученик 4 –– 4 задачи. При проведении серии из 200 испытаний получаются следующие результаты (рис. 2.2). Ученик 1 в среднем затратил T_i = 41000 УЕВ и первым решил R_i = 2,6 задачи из 10, а ученик 8 затратил T_8 = 49400 УЕВ и первым решил R_8 = 0,3 задачи из 10.
Эта модель позволяет изучить зависимость общего времени работы учеников от их количества. Пусть все ученики имеют одинаковые a_i = 0,12 и v_i = 1/9 и на занятии решают 8 задач. Как показывают расчеты 2 ученика это делают в среднем за 34100 УЕВ, 4 ученика –– за 30500, 8 –– за 24300, 16 учеников –– за 22800 УЕВ. То есть при увеличении числа учеников среднее время решения всех задач уменьшается, стремясь к некоторому предельному значению T_min. Это объясняется тем, что при увеличении общего числа попыток, предпринимаемых всеми учениками, возрастает вероятность решения задачи каким–то одним учеником, который затем объяснит его классу.
4. Выводы.
Рассмотренная модель обучения учитывает влияние коэффициента усвоения и скорости совершения учеником интеллектуальных действий. С ее помощью можно обосновать следующие выводы: 1) чем выше коэффициент усвоения и скорость мышления, тем больше количество самостоятельно решенных задач R_i и меньше среднее время T_i требуемое для выполнения задания; 2) при наличии возможности обсуждать решение увеличение числа учеников приводит к тому, что время решения одной и той же последовательности задач уменьшается, стремясь к некоторому пределу T_min.
В статье развиваются идеи, изложенные автором в книге [5], в которой также проанализированы: 1) дискретная и непрерывная однокомпонентная модель обучения; 2) стратегии взаимодействия учителя и ученика; 3) многокомпонентная модель обучения; 4) учет изменения работоспособности ученика; 5) поиск оптимального пути обучения с помощью дискретной и непрерывной моделей; 6) моделирование изучения вопросов, связанных генетической связью; 7) согласование результатов имитационного моделирования процесса обучения с результатами тестирования. Применение рассматриваемых компьютерных моделей позволяет создать цифровую модель ученика, обосновать различные закономерности учебного процесса, изучить зависимость результата обучения от характеристик учебного материала, параметров учеников, длительности и количества занятий и т.д.
Библиографический список
- Атанов Г.А., Пустынникова И.Н. Обучение и искусственный интеллект, или Основы современной дидактики высшей школы. –– Донецк: Изд–во ДОУ, 2002. –– 504 с.
- Ивашкин Ю.А., Назойкин Е.А. Мультиагентное имитационное моделирование процесса накопления знаний // Программные продукты и системы. –– 2011. –– N 1. –– С. 47 – 52.
- Майер Р.В. Двухкомпонентная модель изучения курса: результаты имитационного моделирования // Психология, социология и педагогика. 2014. № 11 [Электронный ресурс]. URL: http://psychology.snauka.ru/2014/11/3835.
- Майер Р.В. Зависимость оптимального времени изучения ЭУМ от их сложности: Моделирование на компьютере // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 9. – С. 16–20. URL: http://www.rae.ru/upfs/414-r5779
- Майер Р.В. Кибернетическая педагогика: Имитационное моделирование процесса обучения: монография. –– Глазов: Глазов. гос. пед. ин–т, 2014. –– 141 с. (URL: http://maier-rv.glazov.net)
- Майер Р.В. Многокомпонентная модель обучения и ее использование для исследования дидактических систем // Фундаментальные исследования: Педагогические науки. –– 2013. –– N 10. –– С. 2524 –– 2528. URL: http://www.rae.ru/fs/519-r32828/
- Майер Р.В. Оптимизация времени изучения элементов учебного материала различной важности: моделирование на компьютере // NB: Педагогика и просвещение. — 2014. – № 4. – С. 51– 63. URL: http://e-notabene.ru/pp/article_13274.html
- Новиков Д.А. Закономерности итеративного научения. –– М.: Институт проблем управления РАН, 1998. –– 77 с.