Математические методы – это тот инструмент современной науки, который позволяет специалистам из многих отраслей находить оптимальные решения стоящих исследовательских проблем. Применение математических методов в психологии в настоящее время широко и активно развивается. Современные информационные технологии значительно расширили границы применения математических методов в психологических исследованиях. Умение самостоятельно проводить первоначальную статистическую обработку данных экспериментального исследования при помощи ЭВМ, а также грамотно подготовить данные для работы со статистическими пакетами является неотъемлемой частью общепрофессиональной компетенции студентов психологических факультетов университетов. Подобные вопросы рассматривались в работах [2], [3], [4], [5], [6].
В психологической практике, как правило, ставиться задача исследования зависимости некоторого признака – зависимой переменной – от влияющих на него факторов – независимых переменных. Подобную зависимость можно выразить в виде математической модели, которую нетрудно построить на основе статистической обработки данных реального психологического эксперимента. Общее название методики построения таких математических моделей – корреляционно-регрессионный анализ.
Все зависимости между переменными делятся на два типа: а) функциональная зависимость; б) статистическая зависимость.
Для функциональной зависимости характерно такое соответствие между зависимой переменной – Y и независимой переменной – Х, при котором каждому значению переменной Y соответствует, как говорят в математике, одно и только одно значение переменной Х. Такое соответствие называется взаимно-однозначным.
Как правило, в реальности редко приходится иметь дело с функциональными связями между переменными. В основном, в ходе эксперимента выявляются статистические зависимости. Это такие зависимости, при которых изменение значений независимой переменной ведет к изменению лишь среднего значения зависимой переменной, а не каждого конкретного.
Описание статистической зависимости возможно несколькими способами. Например, используя всевозможные коэффициенты корреляции. Но большую возможность для интерпретации дает, как говорят в математике, аппроксимация статистической зависимости функциональной. Аппроксимирующая функция – это такая функция, которая наиболее адекватно представляет существующую статистическую зависимость. Методов аппроксимации существует достаточно много, наиболее распространенный, особенно в компьютерных технологиях, – это метод наименьших квадратов. Сущность этого метода заключается в вычислении таких коэффициентов регрессионных уравнений, при которых сумма квадратов отклонений эмпирических значений результативного признака от теоретических, рассчитываемых по найденному уравнению регрессии – минимальна.
График регрессионного уравнения называется линией регрессии. Можно сказать, что она показывает зависимость переменной Y от переменной X в некой идеальной ситуации, в которой отсутствуют случайные, нерегистрируемые факторы.
Регрессионная модель для случая двух переменных (парная регрессия) представляет собой совокупность двух уравнений, являющиеся в простейшем случае уравнениями прямых:
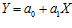
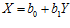 .
.
Таким образом, основной целью регрессионного анализа является расчет численных значений коэффициентов данных уравнений, а также определение их статистической значимости, то есть в подборе такой функциональной зависимости, которая наиболее точно соответствует реальной статистической зависимости между переменными.
Стандартные статистические методы обработки данных включены в состав электронных таблиц, таких как MS Excel и др.; в математические пакеты общего назначения – Mathcad, Mathlab, Maple и т.д. Наиболее мощные методы статистической обработки представлены в специализированных пакетах – STADIA, STATGRAPHICS, SPSS, STATISTIСA и др.
Табличный процессор Microsoft Excel наиболее часто иcпользуется для анализа экономической информации. Также он может быть достаточно удобен для приобретения первоначальных навыков статистической обработки данных психологического или социологического исследования.
Для проведения статистической обработки данных табличный процессор Microsoft Excel имеет программную надстройку «Пакет анализа», включающую в себя большой набор статистических функций. Для проведения полного и качественного статистического анализа такого набора инструментов бывает часто вполне достаточно. Возможности решения психологических задач для студентов-психологов на основе процессора Microsoft Excel рассмотрим на примере выявления взаимосвязи между переменными величинами.
Линейный регрессионный анализ может быть реализован в режиме «Регрессия» надстройки «Пакет анализа» Microsoft Excel. Основное содержание регрессионного анализа для случая двух переменных и интерпретацию результатов рассмотрим на следующих примерах. Сначала рассмотрим случай линейной регрессии.
Пример 1. В классическом исследовании Ф. Гальтона (автора термина «регрессия») был измерен рост 205 родителей и 930 их взрослых детей (см. таблицу 1) [1]. С помощью регрессионного анализа им было проиллюстрировано наличие положительной зависимости между ростом родителей и их детей.
Поставим задачу – найти линейную регрессионную модель, которая выявляет зависимость между ростом родителей и ростом их детей, используя инструменты пакета анализа MS Excel.
Таблица 1. Зависимость роста детей от роста их родителей
| Рост родителей |
Рост детей в дюймах |
Всего | |||||||
|
60,7 |
62,7 |
64,7 |
66,7 |
68,7 |
70,7 |
72,7 |
74,7 |
||
|
74 |
4 |
4 |
|||||||
|
72 |
1 |
7 |
11 |
17 |
20 |
6 |
62 |
||
|
70 |
1 |
2 |
21 |
48 |
83 |
66 |
22 |
8 |
251 |
|
68 |
1 |
15 |
56 |
130 |
148 |
69 |
11 |
430 |
|
|
66 |
1 |
15 |
19 |
56 |
41 |
11 |
1 |
144 |
|
|
64 |
2 |
7 |
10 |
14 |
4 |
37 |
|||
| Всего |
5 |
39 |
107 |
255 |
287 |
163 |
58 |
14 |
928 |
Решение. Открываем рабочий лист MS Excel (рис. 1) и заносим данные из исходной таблицы (хотя эта процедура достаточно утомительна, нам придется с этим смириться и использовать некоторые хитрости MS Excel).
|
Рис. 1. Ввод данных |
Рис. 2. Окно «Регрессия» |
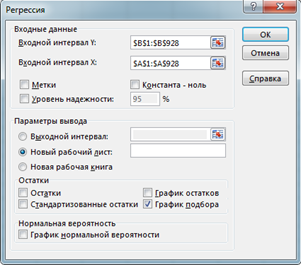
Пакет анализа MS Excel запускается командой Анализ данных в меню Сервис. Затем, в открывшемся диалоговом окне кликаем строку Регрессия. В новом диалоговом окне Регрессия задаем ссылки на введенные данные для входных интервалов Х и Y (рис. 2). Кликнув кнопку Ok, открываем окно вывода результатов, в котором мы видим коэффициенты уравнения регрессии (рис. 3)
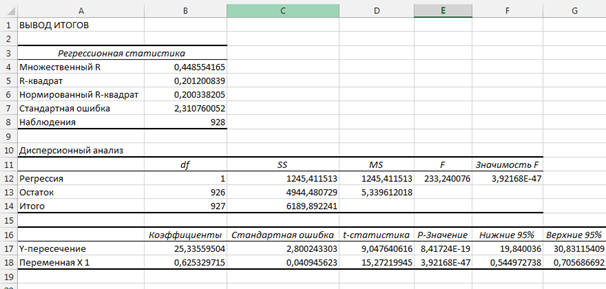
Рис. 3. Окно вывода результатов
Таким образом, искомое уравнение регрессии, которое выражает зависимость роста детей Y от роста их родителей Х имеет вид:
Y = 0,625X + 25,336.
Иная методика расчета коэффициентов уравнения регрессии в MS Excel может быть применена для случая нелинейной регрессии.
Пример 2.
У восьми подростков психолог сравнивает баллы по третьему субтесту теста Векслера (переменная X) и оценки по алгебре (переменная Y).
| Значения X | 8 | 18 | 18 | 10 | 16 | 10 | 8 | 14 |
| Значения Y | 2 | 3 | 4 | 5 | 4 | 4 | 3 | 5 |
Психолога интересует вопрос: на сколько баллов повысится успешность решения третьего субтеста теста Векслера, если оценки по алгебре повысятся на один балл? Кроме того, его интересует вопрос, будет ли повышение успешности решения третьего субтеста теста Векслера на один балл влиять на повышение оценок по алгебре? [1]
Решение. Ответы на все эти вопросы даст нам метод регрессии в Microsoft Excel. Применив технологию построения линейной регрессионной модели мы получим уравнение регрессии Y на X:
Y= 3 + 0,06Х,
для которого коэффициент смешанной корреляции будет равен 0,05. С помощью данного коэффициента мы определяем точность аппроксимации: чем ближе его значение к 1 и дальше от нуля, тем точнее уравнение регрессии отражает реальную зависимость. В нашем случае коэффициент корреляции слишком мал, что говорит о неадекватности полученной регрессионной модели.
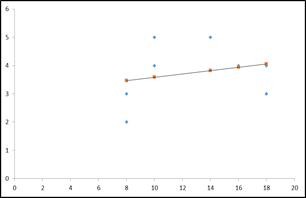
Наиболее адекватную модель мы сможем выбрать с помощью метода построения диаграмм зависимостей между переменными (рис. 4) и подбором аппроксимирующей
кривой. В Microsoft Excel представлена возможность выбора одного из пяти видов аппроксимирующих кривых: линейная, степенная, полиномиальная, экспоненциальная и логарифмическая.
|
Рис. 4. Аппроксимация данных прямой |
Рис. 5. Аппроксимация данных кривой 4-й степени |
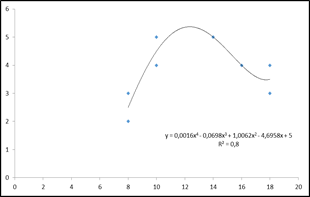
Для данной задачи, если исходить из значения коэффициента смешанной корреляции (равен 0,8), наиболее точно соответствует реальной зависимости между переменными полиномиальная кривая четвертой степени (рис. 5). Уравнение регрессии в этом случае имеет вид:
Y = 0,002Х4 – 0,07Х3 + 1,007Х2 – 4,7Х + 5
Далее, аналогично, найдем уравнение регрессии X на Y.
Наиболее адекватная регрессионная модель получается при аппроксимации данных полиномиальной кривой третьей степени (рис. 6; надо учесть, что в MS Excel зависимая переменная всегда у, а независимая всегда х ) с уравнением
Х= – 0,2Y3 – 0,2Y2 + 9Y – 8
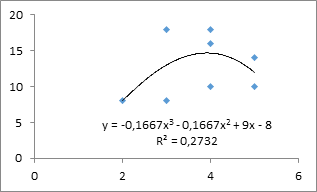
Рис. 6. Аппроксимация данных кривой 3-й степени
Построив регрессионные модели, мы можем ответить на оба вопроса задачи. Так, согласно Полученным моделям увеличение значений одной переменной приводит к увеличению значения другой переменной только при низких и средних результатах, в то время как высокие показатели по одному параметру вовсе не определяют высоких показателей по другому параметру.
Библиографический список
-
Ермолаев О.Ю. Математическая статистика для психологов. М.: МПСИ, 2002. 336 с.
-
Трухманов, В.Б., Трухманова, Е.Н. О некоторых методах компьютерной обработки экспериментальных данных // Вестник Омского государственного педагогического университета [Электронный научный журнал]. – Выпуск 2006 г. – Режим доступа: URL:http://www.omsk.edu/volume/2006/comp-edu/
-
Трухманов В.Б. Компьютерная среда как средство формирования навыков анализа экономико-математических моделей // Приволжский научный вестник. 2014. № 3-2(31). С. 118-121.
-
Трухманов В.Б., Трухманова Е.Н. К вопросу о применении компьютерных технологий в социально-психологическом эксперименте // Труды СГА. 2009. №11. С. 117-123.
-
Трухманова Е.Н. Личностные особенности подростков-сирот и подростков, оставшихся без попечения родителей как фактор их дезадаптации: автореф. дисс. … канд. псих. наук. Москва, 2004. 26 с.
-
Трухманова Е.Н. Личностные особенности подростков-сирот и подростков, оставшихся без попечения родителей как фактор их дезадаптации (на материалах сельских детских домов): дисс. … канд. псих. наук. Москва, 2004. 288 с.