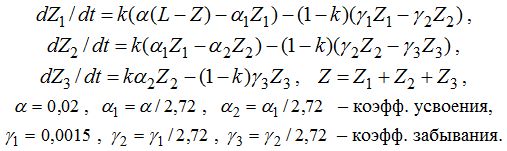Отношение к использованию методов математического и имитационного (или компьютерного) моделирования для изучения дидактических систем неоднозначное. Существуют две противоположные точки зрения: 1) обучение – творческий стохастический процесс, в котором нельзя ничего стандартизировать, измерить, выразить в числовом виде, поэтому создать математическую или компьютерную модель принципиально невозможно; 2) обучение – жестко детерминированный процесс, подобный технологическому, поэтому возможно создание технологии обучения, приводящей к заданному результату, который может быть предсказан с помощью компьютерной модели.
Истина находится посередине. Конечно же дидактический процесс не является жестко детерминированным: на его результат влияют различные случайные факторы, которые учесть сложно. С другой стороны, ориентируясь на качественную модель среднестатистического ученика, возможно создать стандарт, учебную программу или учебник, по которым будут успешно учиться тысячи школьников. Учитель, готовясь к уроку, также моделирует ситуацию, выбирая при этом такие методы обучения, которые позволят ученикам усвоить рассматриваемый материал за определенное время.
Возможность использования математических и имитационных моделей обучения обусловлена тем, что многие величины, характеризующие состояние системы “учитель–ученики” (уровень требований L учителя, количество знаний учеников Z) поддаются измерению. Для определения количества информации в тексте может быть использован семантический метод, состоящий в подсчете смысловых единиц, понятий, связей между ними и т.д. За единицу измерения количества знаний (то есть усвоенной школьником информации) может быть выбрано понятие [1, 3], элементарное суждение или математическая формула. Рисунок несет в себе столько информации, сколько содержит его наиболее краткое словесное описание. Каждый элемент учебного материала (ЭУМ) характеризуется сложностью, которая пропорциональна затратам усилий или времени, требуемым для его усвоения.
Информационная емкость понятия равна количеству его связей (или линков) с другими, ранее изученными понятиями [3, с. 249–259]. В работе [1] утверждается, что в среднем емкость одного понятия равна трем линкам. Для измерения объема умений М.П.Карпенко предлагает подсчитывать степы. “Степ (шаг) – единица измерения емкости умения, представляющая собой единичный шаг алгоритма умения. Средний объем одного умения равен 4 степам” [1]. Оказывается, что “время усвоения в учебном процессе 1–го умения в 3 раза больше времени усвоения 1–го понятия”, а “на усвоение одного степа в 2,25 раз времени затрачивается больше, чем на усвоение одного линка”. Если соотнести время усвоения понятия и умений, то можно ввести универсальную единицу оценки объема учебной информации – приведенное понятие [1, 3].
В принципе могут быть определены и другие характеристики дидактических систем. Например, известно, что скорость чтения вслух не может превышать 150 слов в минуту. Чтобы оценить уровень требований учителя можно методом экспертных оценок оценить сложность каждого ЭУМ по шкале 1–5, и просуммировать получившиеся значения. Все это позволяет приближенно измерить количество информации в учебнике или лекции, определить скорость усвоения знаний, построить математическую, а затем и компьютерную модели.
Хорошо известны физические (гидравлические) модели обучения, в которых роль информации играет вода, во время занятия перетекающая из резервуара (учителя) в сосуд (ученика), а после занятия медленно вытекающая из сосуда. В книгах [2, 4] проанализированы некоторые математические модели дидактических систем. Имитационные модели представляют собой компьютерные программы, “позволяющие имитировать на ЭВМ поведение отдельных элементов системы S и связей между ними в течение заданного времени моделирования” [6, c. 49]. Они применяются для изучения сложных систем, законы функционирования которых неизвестны, но имеется информация об алгоритмах работы отдельных подсистем и о связях между ними. При этом значения параметров элементов системы и характеристики связей выявляются в ходе имитационного эксперимента на ЭВМ. Недостаток этого метода – в отсутствии надежных способов оценки адекватности имитационных моделей [6, с. 49].
Имитационное моделирование сложных систем занимает промежуточное место между качественным моделированием (то есть построением словесной модели) и компьютерным моделированием детерминированных физических, химических и иных процессов. Для изучения дидактических систем используют непрерывные модели, основанные на численном решении системы дифференциальных уравнений [2, 4] и дискретные модели, в которых ученик моделируется вероятностным автоматом [4]. Также применяют мультиагентный подход, при котором каждый учащийся заменяется программным агентом, функционирующим независимо от других агентов.
Сформулируем основную задачу имитационного моделирования процесса обучения: зная параметры учащихся, характеристики используемых методов и учебную программу (распределение учебной информации), нужно определить количество знаний или уровень сформированности навыка у учащихся на любом этапе обучения [4]. Может быть решена оптимизационная задача, заключающаяся в нахождении распределения учебного материала, уровня требований учителя, длительности занятий, при которых количество знаний учащихся в конце обучения достигнет заданного или максимального значения, а сам процесс обучения будет удовлетворять наложенным ограничениям.
Р. Шеннон говорит о имитационном моделирования как интуитивном искусстве [7, c. 33], в котором большое значение имеют различные аналогии и ассоциации. Система разбивается на подсистемы, каждая из которых имеет свои параметры, определяются функциональные зависимости или законы функционирования каждой подсистемы, накладываемые на них ограничения и целевые функции. Само моделирование имеет эволюционный характер и приводит к получению ряда моделей, каждая из которых является развитием предыдущей. Возможно построение моделей на основе принципиально различных подходов с последующим сравнением результатов моделирования. Моделирование – творческий процесс, требующий решения многомерной задачи с большим числом переменных. В ходе вычислительного эксперимента “имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры, последовательности протекания во времени, что позволяет получить информацию о состоянии системы S в заданные моменты времени” [6, с. 5–6].
Большое значение при построении модели имеет вопрос о выборе коэффициентов. Р. Шеннон отмечал, что “почти в любой имитационной модели многие переменные рождаются на основании весьма сомнительных данных. Во многих случаях их значения могут быть определены только на основе предположений опытного персонала или с помощью весьма поверхностного анализа некоторого минимального объема данных” [7, c. 48]. Поэтому важно проверить модель на чувствительность к изменению исходных данных и параметров. Для анализа результатов следует оперировать понятиями нечеткой логики.
С целью сохранения общности выводов время и уровень L требований учителя (а значит и количество знаний Z ученика) следует измерять в условных единицах. Например, можно считать, что 45–минутный урок длится 100 усл. ед. времени (УЕВ), тогда на 1 минуту приходится 2,22 УЕВ. Если объемы информации, изучаемой на 1, 2 и 3 уроках соотносятся как 0,8:1,1:1,3, то можно считать, что на этих уроках рассматривается 89, 110 и 130 элементов учебного материала (ЭУМ). Понятно, что от выбора условных единиц измерения времени и информации зависят значения коэффициентов усвоения и забывания, характеризующие быстроту изменения количества знаний у ученика. В педагогической практике встречаются разнообразные ситуации, находящиеся между двумя крайностями: 1) ученик так плохо усваивает материал, что к концу урока помнит 0,05L; 2) ученик так хорошо усваивает материал, что к концу занятия помнит 0,95L. Дидактическая система является самонастраивающейся, учитель организует обучение так, что к концу урока ученик усвоил 60–80 % всей сообщенной учителем информации. Коэффициенты усвоения и забывания ученика выбирают так, чтобы они соответствовали реальной ситуации.
В статье [5] предложена компьютерная программа, моделирующая процесс обучения, основанная на решении системы дифференциальных уравнений (при обучении k = 1, при забывании k = 0):
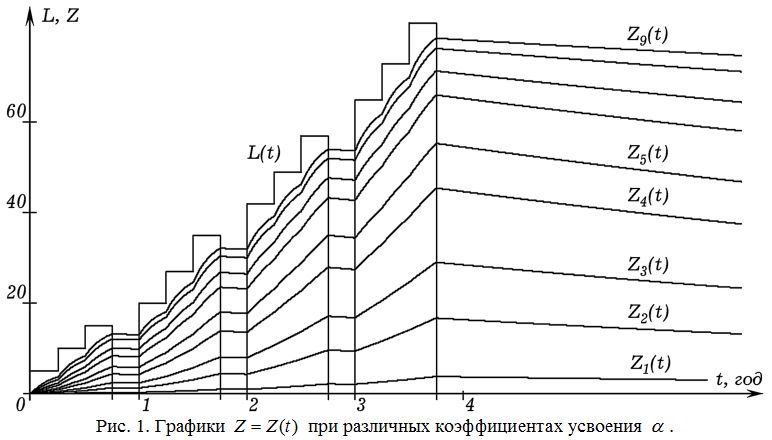
Здесь Z_1, Z_2, Z_3 – количества непрочных знаний, знаний средней прочности (умений) и прочных знаний (навыков) ученика. Коэффициент усвоения численно равен скорости увеличения соответствующих знаний ученика при его отставании от требований учителя на 1 ЭУМ: L–Z=1. Коэффициент забывания равен ln(2)/T, где T – время забывания половины усвоенной информации в УЕВ.
Программа моделирует изучение некоторой дисциплины в течение 4 лет (9 месяцев обучение, 3 месяца каникулы). Результат моделирования зависит от параметров ученика; на рис. 1 показаны получающиеся графики зависимостей Z = Z(t) в случаях, когда коэффициент усвоения равен 0,0002; 0,001; 0,002; 0,004; 0,006; 0,01; 0,014; 0,022; 0.03. Понятно, что на практике реализуется всевозможные ситуации, однако большинство учеников в результате обучения усваивают 60–80 % требуемых на оценку 5 знаний. Это соответствует коэффициентам усвоения 0,01 – 0,03. Поэтому в данном случае имеет смысл коэффициент усвоения выбирать 0,02.
В ходе имитационных (вычислительных) экспериментов решаются следующие задачи: 1) исследуется поведение конкретной математической модели при различных параметрах и входных данных; 2) устанавливается возможность ее использования для адекватной имитации процесса обучения; 3) подбираются коэффициенты, при которых модель дает результаты, соответствующие здравому смыслу, результатам тестирования и т.д.
Библиографический список
- Богданов, И.В. Учебная информация и единицы ее измерения // Труды СГУ. М.: СГУ, 2002.
- Имаев, Д.Х., Котова, Е.Е. Моделирование и имитация процесса обучения с разделением дидактических ресурсов: Динамический подход. – СПб: Изд–во СПбГЭТУ ЛЭТИ, 2014. – 111 с.
- Карпенко, М.П. Телеобучение. – М.: СГА, 2008. – 800 с.
- Майер, Р.В. Кибернетическая педагогика: Имитационное моделирование процесса обучения.– Глазов: Глазов. гос.пед.ин–т, 2014. – 141 с.
- Майер, Р.В. Компьютерные модели скачкообразного и непрерывного увеличения знаний при обучении // International Journal of Open Information Technologies. – vol. 3. – no. 9. – 2015. – С. 9 – 13.
- Харин, Ю. С. Основы имитационного и статистического моделирования: учебное пособие / Ю. С. Харин, В. И. Малюгин, В. П. Кирлица и др.– Минск: Дизайн ПРО, 1997. – 288 с.
- Шеннон, Р. Имитационное моделирование систем: искусство и наука. – М.: Мир, 1978. – 302 с.