Об аналогии
Возможно, не существует открытий ни в элементарной,
ни в высшей математике, ни даже, пожалуй, в любой другой
области, которые могли бы быть сделаны… без аналогии
Д. Пойа
Аналогия в обучении информатике, конечно, используется. В основном – просто для объяснения нового. Например, когда учитель вместо – «просматриваем элементы массива, начиная с элемента с индексом один, пока очередной элемент не станет равным данному числу» говорит – «бежим от начала массива, пока не встретим наше число». Такой «человеческий» язык помогает уловить суть. С меньшими затратами, как для учителя, так и для ученика. Или, например, когда решаются несколько изменённые задачи. Находили минимум в том же массиве, а сейчас находим максимум. Да, аналогия есть. Но на репродуктивном, очевидном уровне.
Важно показать силу аналогии более высокого уровня. В науке это мощное средство открытий и источник гипотез. В истории множество примеров. Чего стоит одна бионика. Здесь только и занимаются, как «всматриваются» в природу и «списывают» у неё изобретения.
И в информатике есть такие примеры, доступные для учеников. Пусть и редкие. Так известная задача о коммивояжёре имеет три «природных» алгоритма решения [1]. Первый имитирует отжиг металлов. Второй – биологическую эволюцию. Третий – поведение муравьёв. Изучение этих алгоритмов позволит ученикам увидеть и почувствовать, как делаются открытия, на основе аналогии, которая подсказывает и направляет.
Задача коммивояжёра
Имеется n городов, стоимости проезда между которыми известны. Коммивояжёру, бродячему торговцу, необходимо начать путешествие от первого города, посетить все остальные n-1 городов по одному разу и вернуться обратно. При этом маршрут торговца должен быть самый дешёвый.
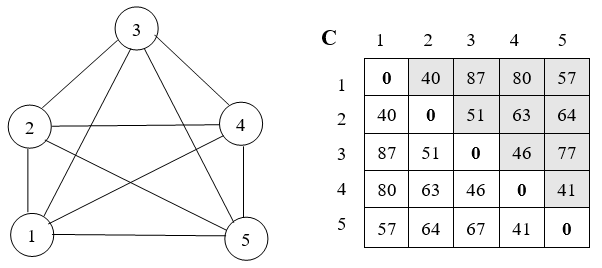
Стоимости проезда между городами удобно хранить в таблице n*n. В первой строке хранятся стоимости проезда от первого города до всех остальных, во второй строке – от второго города до всех остальных и т.д. Скажем, для пяти городов таблица может быть такой, как на рис. 1.
Первый, очевидный, универсальный способ решения. Перебрать все возможные маршруты торговца, а их (n-1)!, и выбрать маршрут с минимальной стоимостью. Но для больших значений n этот алгоритм бессилен, так как работает непозволительно долго.
Что делать в таких случаях? Искать быстрые приближенные алгоритмы. Они не всегда выдают точное решение, но стремятся получить близкое к нему.
В поисках идеи
Факт. Многие изобретения «списаны» с природы. Так ещё Леонардо да Винчив 15 веке старался подражать природе. Наблюдал за полетом птиц и строил летательные аппараты. И даже написал книгу «О летании птиц», в которую до сих пор заглядывают и современные конструкторы аэропланов.
Другой пример. Это было в годы первой мировой войны. Британский флот получил на вооружение гидрофоны – приборы для обнаружения германских подводных лодок по шуму винтов. Сторожевые корабли вышли в море и… изобретение оказалось бесполезным.
Первые гидрофоны походили на большую докторскую трубку. Во время хода корабля движение воды у приемного отверстия создавало шум. Этот шум заглушал звук винтов преследуемой подводной лодки. Приходилось останавливаться и прекращать преследование.
Физику Роберту Вуду было известно, что тюлени отлично слышат при движении. Он предложил гидрофоны, которые имели форму ушной раковины тюленя. И гидрофоны стали «слышать», даже на полном ходу корабля.
Ещё одно открытие, «подсмотренное» у природы. Английскому инженеру Сэмюэлю Брауну было поручено построить через реку Твид железнодорожный мост. Мост должен был быть прочным и в то же время не слишком дорогим. Как-то, прогуливаясь по своему саду, Браун заметил паутину, протянутую через дорожку. В ту же минуту ему пришла в голову мысль. Точно так же можно построить и висячий мост на железных цепях.
Примеров очень и очень много [2]. Вернёмся к задаче о коммивояжёре. Оказывается, и её решение можно позаимствовать у природы [3, 4, 5].
Алгоритм отжига
Наблюдение. Металлическая деталь отлита. Однако не всегда её охлаждение происходит равномерно. Атомы «застывают» в случайных положениях. Возникают неоднородности, напряжения и изломы в различных местах. Где-то деталь более пластичная. Где-то более хрупкая. Что делают? Металл отжигают. Нагревают до определённой температуры и медленно охлаждают. При высокой температуре атомы, выстроившиеся в «кривую» кристаллическую решетку, покидают свои места. Стремятся занять правильное положение между другими атомами. Так чтобы их общая энергия колебательного движения стала минимальной. Температура медленно понижается. Атомы становятся менее подвижными. Их положения фиксируются. Происходит выравнивание кристаллической решётки. Неоднородности исчезают.
Аналогия. Возьмём произвольный маршрут торговца. Скорее всего его стоимость не минимальна. Города расположены не в том порядке. Какие-то можно переставить и стоимость уменьшится.
Ситуация та же, что и в только что отлитой детали. Скорее всего энергия колебательных движений её атомов в некоторых местах не минимальна. Атомы застыли в «кривой» кристаллической решётке. Если её исправить, то энергия уменьшиться.
Города – это атомы. Маршрут – кристаллическая решётка. Стоимость – энергия. Перестановка городов в маршруте – движение атомов по кристаллической решётке. А раз ситуация та же, то можно попробовать отжечь наш «неправильный» маршрут до «правильного» или близкого к нему.
Алгоритм.
1. Берём какой-нибудь произвольный маршрут – s.
2. Находим его стоимость – e(s).
3. Считаем этот маршрут наилучшим – sbest:=s, ebest:=e(s).
4. Задаём начальную высокую температуру – t:=t0. А также комнатную – tlast, до которой и будем понижать.
6. Выбираем коэффициент р, который будет отвечать за скорость понижения температуры. Например, р:=0,9. А также k – время, на протяжении которого мы не будем менять температуру. Например, k:=100.
7. Пока температура больше комнатной – t > tlast.
Повторяем k раз при данной температуре t.
*Получаем новый маршрут snew, переставив два случайных соседних города в текущем маршруте s.
*Находим стоимость нового маршрута – e(snew).
*Если стоимость нового маршрута меньше стоимости текущего – e(snew)<e(s), то принимаем новый маршрут – s:=snew, e(s):= e(snew). То есть к «хорошему» маршруту переходим в любом случае.
*Иначе генерируем случайное число x из промежутка (0;1). И если x<t/t0, то и такой маршрут также принимаем – s:=snew, e(s):= e(snew). То есть к более «плохому» маршруту переходим не всегда, а с вероятностью t/t0. Эта вероятность будет уменьшаться с понижением температуры t.
*Если очередной маршрут лучше – s<sbest, то запоминаем его – sbest:=s, ebest:=e(s).
Уменьшаем температуру – t:=p*t.
8. Выводим наилучший маршрут и его стоимость – sbest и ebest.
Коээфициенты t0, tlast, p и k подбираем эмпирически. Необходимо попробовать разные значения и выбрать наилучшие.
Методическое замечание. Аналогию здесь и далее ученики, по возможности, должны увидеть сами и даже предложить свой вариант алгоритма. А вот уже его уточнение и детализация – совместная работа. Программирование не должно представлять сложности – цикл в цикле, простые условия и строки. И ещё, в реальном алгоритме, вероятность принятия «плохого» маршрута вычисляется по другой формуле. А именно, exp(-(e(snew)-e(s))/t). То есть она зависит не только от температуры, но и от того, насколько «плох» маршрут. При одной температуре более «плохие» маршруты принимаются реже. Но мы взяли более простой вариант. Тот, который может предложить и сам ученик.
Генетический алгоритм
Наблюдение. Жизнь на нашей планете развивалась от одноклеточных организмов и до первых животных и людей. Так утверждает эволюционная теория. Действовал естественный отбор и генетическая наследственность. Наиболее приспособленные организмы чаще выживали, чем менее приспособленные. «Срещивались», обмениваясь генами, и приносили потомство. При этом потомки наследовали признаки своих родителей. Иногда происходили мутации, изменение некоторых генов. Например, под воздействием радиации. Организмы приобретали новые качества. Всё повторялось из поколения в поколение.
Аналогия. Пусть у нас есть несколько маршрутов для коммивояжёра. Разумеется, у одних стоимость меньше, у других больше. Представим, что это организмы и запустим в этом виртуальном мире эволюцию. Наиболее приспособленные маршруты – с меньшей стоимостью – будут выживать, «скрещиваться» и давать новые маршруты. Те иногда мутировать. Наш мир развиваться. В нём будут появляться всё лучшие и лучшие маршруты. Через достаточно долгое время остановим эволюцию и выберем наиболее приспособленный организм в поколении. Есть надежда, что это будет если не самый лучший (дешёвый) маршрут, но близкий к нему. Вершина эволюции.
Алгоритм.
1. Инициализация. Создаём начальное поколение. Случайным образом генерируем m различных маршрутов.
2. Оценка. Вычисляем приспособленность каждого маршрута текущего поколения. Приспособленность маршрута равна единице, поделённой на его стоимость. Чем меньше стоимость, тем больше приспособленность.
3. Отбор. Из текущего поколения выбираем наиболее приспособленные маршруты, которые будут участвовать в создании следующего поколения. Остальные вымирают. Используем для этого «метод рулетки».
Для обычной рулетки у шарика одинаковые шансы остановиться в любом из секторов. Разделим рулетку на неравные секторы. Тогда вероятность того, что шарик остановится в широком секторе велика, а в узком мала. Пусть каждый сектор нашей «кривой» рулетки отвечает за один из маршрутов. Чем больше приспособленность маршрута, тем больший сектор он получает.
Запускаем рулетку m раз. Получаем m маршрутов. Они и будут участвовать в следующем этапе эволюции. Некоторые из маршрутов будут выбраны несколько раз, а некоторые – ни разу. Но в основном, это будут наиболее приспособленные. Мы оставляем шанс и неприспособленным организмам, так как и они могут иметь полезные качества.
4. Скрещивание. Все m отобранных маршрутов произвольно разбиваем на пары и «скрещиваем».
Пара родителей даёт двух потомков. Но не каждая. Это происходит с некоторой вероятностью скрещивания pc. Обычно 0,5<pc<1. То есть способными дать потомство оказываются от 50 до 100% родителей.
Если родители получили потомков, то эти потомки и переходят в новое поколение. Иначе переходят сами родители. Таким образом, в новом поколении снова m маршрутов.
Как происходит скрещивание? Если случайно взять точку разреза и обменять части маршрутов справа от неё, то возникает проблема.
Так родители:
(1 2 3 4 5 | 6 7 8 9)
(1 5 3 6 8 | 9 7 2 4)
дают таких потомков:
(1 2 3 4 5 | 9 7 2 4)
(1 5 3 6 8 | 6 7 8 9)
Может оказаться, что в потомках некоторые города будут повторяться, а некоторые вообще отсутствовать. Дети уже не будут маршрутами, так как города должны быть все и по одному разу.
Используем другой способ. Снова случайно выбираем точку разреза. В первого потомка копируем из первого родителя все города до этой точки. А затем просматриваем второго родителя и записываем в потомка только те города, которых в нём ещё нет. Точно так же строится второй потомок. В него копируем из второго родителя все города до точки разреза. Просматриваем первого родителя и записываем в потомка только те города, которых в нём ещё нет.
Например, родители:
(1 2 3 4 5 | 6 7 8 9)
(1 5 3 6 8 | 9 7 2 4)
дают таких потомков:
(1 2 3 4 5 | 6 8 9 7)
(1 5 3 6 8 | 1 2 7 9)
5. Мутация. Новое поколение мутирует. Но не всё маршруты. Это происходит с некоторой вероятностью мутации pm. Обычно pm<0,05. То есть мутирует только около 5%.
Как происходит мутация? В маршруте меняются местами два случайных города. Скажем, был маршрут (1 2 3 4 5 6 8 9 7), а стал (1 2 9 4 5 6 8 3 7).
6. Завершение алгоритма. Итак, в результате оценки, отбора, скрещивания и мутации образуется новое поколение из m маршрутов. И всё повторяется заново, с этапа оценки. Поколение сменяет поколение. До тех пор, пока не пройдёт n поколений. В последнем берём самый приспособленный (дешёвый) маршрут. Он и будет решением задачи.
Параметры m, n, pc и pm подбираем эмпирически. Очевидно, например, чем больше маршрутов в поколении, тем медленнее алгоритм. Но, быть может, поколение будет более разнообразным – и в нем возникнет более приспособленный маршрут.
Муравьиный алгоритм
Наблюдение. Муравьи, пожалуй, самые общественные насекомые. Один муравей – в поле не воин. А вот уже их колония справляется со многими задачами. Некоторые ученые даже называют такие колонии «коллективным разумом». Например, группа муравьев прекрасно умеет находить кратчайший путь к пище.
Вначале муравьи двигаются произвольно. При этом оставляя за собой дорожки из особых веществ – феромонов. Нашедшие самый короткий путь к «кормушке» успевают по нему пробежать больше раз. Путь становится всё заметнее. Привлекает муравьев. Они всё чаще сворачивают на него. На остальных путях феромон постепенно испаряется и они исчезают. И вот, через какое-то время, большинство муравьёв передвигаются по одному кратчайшему пути.
Аналогия. Очевидная. Запустим муравьев из первого города. И пусть они, вместо коммивояжёра, бегают по различным возможным маршрутам и возвращаются обратно. На дешёвых маршрутах оставляют больше феромона. На дорогих – меньше. Через некоторое время их остановим. Наилучший маршрут, который они найдут, и будем считать решением задачи.
Алгоритм.
1. Строим какой-нибудь случайный маршрут. Считаем его наилучшим.
2. Задаем начальный уровень феромона. Вводим ещё одну таблицу F размерности n*n. Для хранения количества феромана между городами. В каждую клетку записываем одно и то же небольшое положительное число. Считаем, что вначале между любыми двумя городами одинаковое количество феромона. Поэтому при первом запуске муравьи будут двигаться произвольно, «не принюхиваясь».
3. Выбираем коэффицент испарения феромона p, из промежутка (0;1). Чем больше возьмём p, тем быстрее будет происходить испарение.
4. Повторяем k раз (k можно считать временем жизни муравьиной колонии).
* Запускаем m муравьёв из первого города. Они пробегают оставшиеся n-1 городов по одному разу и возвращаются обратно. Для каждого находим свой маршрут и его стоимость.
Как муравей, путешествуя, определяет следующий город? Во-первых, этот город должен быть ещё не посещённым. Во-вторых, на пути к нему должно быть больше феромона. Применяем знакомый метод «рулетки». Возможным городам ставим в соответствие сектор рулетки. Чем больше феромона, тем больше сектор. Запускаем рулетку. Случай выбирает один город.
* Если какой-то муравей нашёл лучший маршрут, чем ранее, то запоминаем этот маршрут и его стоимость.
* Увеличиваем феромон вдоль всех маршрутов, по которым прошли муравьи. На лучших (дешёвых) маршрутах оставляем больше феромона. Берём первого муравья, просматриваем рёбра из его маршрута и на каждое добавляем феромон. По формуле F[i,j]:=F[i,j]+Q/L, где L – стоимость маршрута, Q – некоторая константа. Затем берём второго муравья и т.д.
* Испаряем феромон на всех рёбрах между городами. По формуле F[i,j]:=(1-p)*F[i,j]. Тем самым постепенно удаляем рёбра, которые меньше всего используются.
5. Выводим наилучший маршрут и его стоимость.
Параметры p, k, m и Q подбираем эмпирически.
Библиографический список
- Джонс М.Т. Программирование искусственного интеллекта в приложениях. – М.:ДМК-Пресс, 2004.
- Альтшуллер Г.С. Как научиться изобретать / Тамбов: Книжное издательство, 1961.
- Гладков Л. А., Курейчик В. В, Курейчик В. М. Биоинспирированные методы в оптимизации: монография. – М: Физматлит, 2009.
- Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. – М: Горячая линия-Телеком, 2008.
- Кирсанов М. Н. Графы в Maple. М.: Физматлит, 2007.