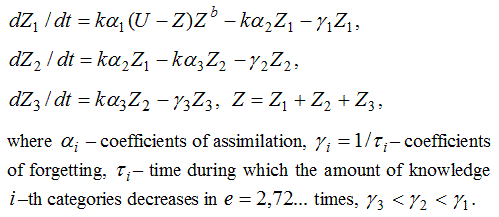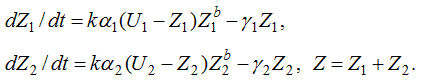Introduction
Development of an education system demands creating of the theoretical foundations of didactics with attraction both humanitarian (psychology), and the exact sciences (mathematics, cybernetics). Among methods of research of didactic systems the important place is taken by methods of mathematical and imitating (computer) modeling. Their essence consists that the real pedagogical system is replaced with abstract model, – some idealized object which behaves like studied system. Such model can be a set of logical rules, the mathematical equations [1, 5, 6, 8, 9] or the computer program [2 - 4, 6], allowing to carry out a series of experiments at various parameters, entry conditions and external influences. Changing the initial data and the model parameters it is possible to study the development of the didactic system and determine its state at the end of training.
We will formulate the main objective of imitating modeling of process of learning: knowing parameters of pupils, characteristics of used methods and the training program (distribution of educational information), to define level of knowledge (or formation of skill) at pupils at the end of training. The discrete and continuous models which are based on automatic approach and the solution of the differential equations [1, 4, 8] are known. In certain cases is using multi-agent modeling at which each pupil is replaced with the program agent which functioning irrespective of other agents [3]. Also there are the imitating models using networks of Petri, genetic algorithms, matrix modeling [1 – 4].
All this viewed models have common fault: they don’t consider that the elements of learning material (ELM) acquired by the pupil aren’t equal. Those ELM which are included in activity of the pupil, turn into strong (durable) knowledge and forgotten more slowly. The ELM which aren’t included in activity, turn into weak (not strong) knowledge and forgotten quicker. In the course of educational activity weak knowledge gradually becomes strong. The problem consists in creating the imitating model of training which take into account distinction in speed of forgetting of various ELM and transition of weak knowledge in the category of strong knowledge [7].
1. Multi-component model of training: general ideas
It is known that process of assimilation and memorizing of given information consists in establishment of associative links between new and available knowledge. As a result acquired knowledge becomes stronger and is forgotten much more slowly. Repeated use of knowledge leads to formation of the pupil of the corresponding skills which remain a long time. The assumption was made: computer model will correspond more precisely to real process of training if it will be consider that: 1) strength or durability of assimilation of various ETM isn’t identical therefore all ELM should be divided into some categories; 2) strong (trustworthy or solid) knowledge is forgotten significantly more slowly than the weak; 3) weak knowledge at their use by the pupil gradually becomes strong.
We will designate through U – the level of requirements shown by the teacher which equal to quantity Z_0 of transmitted ELM. Let Z – total knowledge of the pupil which include knowledge of the first, second and third categories: Z=Z_1+Z_2+Z_3. Thus Z_1 – quantity of the most weak knowledge of the first category with high coefficient of forgetting, and Z_3 – quantity of the strongest knowledge of the third category with low coefficient of forgetting. Coefficients of assimilation characterize speed of transition of knowledge (i-1)-th categories in knowledge i–th categories. The offered three-component model of training is expressed by system of the equations:
While there is a training (k=1), the speed of increase in weak knowledge of the pupil is proportional: 1) differences between level of requirements of the teacher U and the general level of knowledge Z; 2) to amount of already available knowledge Z in degree b. The last is explained by that existing of knowledge promotes establishment of new associative links and memorizing of new information. If the increase of knowledge of pupil is significantly less than their total quantity then b=0. When training stops (k=0), Z decreases due to forgetting. The result of training is characterized by a total quantity of the acquired knowledge Z and coefficient of strength P=(Z_2/2+Z_3)/Z. If all knowledge acquired during training is weak (Z_1=Z, Z_2 = Z_3=0), then coefficient of strength P=0. It is necessary to aspire to a situation, when all acquired knowledge strong (Z_3=Z, Z_1=Z_2=0), then P=1. With long-term learning of one theme the quantity of knowledge Z increases to U, also there is an increase of quantity of strong knowledge Z_4 and coefficient of strength P.
2. Model use in the analysis of concrete situations
Let analyze some situations which are arising in the pedagogical practice.
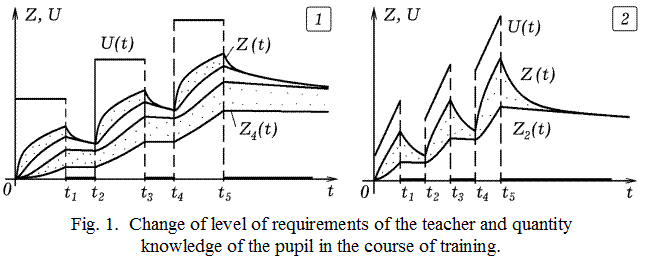
Situation 1. The teacher conducts three lessons, level of requirements during each lesson is set: U_1, U_2, U_3. We will study process of training of the pupil by means of four-component model. Results of modeling are presented in fig. 1.1. It is visible that during training the total of knowledge Z of the pupil increases, part of weak knowledge become stronger. During breaks and after training level of weak knowledge Z_1 quickly decreases, and strong knowledge Z_4 is forgotten significantly more slowly.
Situation 2. The teacher conducts three lessons, level of requirements U(t) during i–th lesson increases in accordance with the equations
Let analyze training process by means of two-component model which is expressed by the equations:
Results of modeling are given in fig. 1.2. At each lesson the teacher demands from pupils: 1) possession of the material studied at the previous lessons; 2) assimilation of new information. During training weak knowledge becomes strong (solid) and after training is forgotten significantly more slowly.
Situation 3. The pupil within 11 years studies at school. The coefficient of assimilation of information during of training increases and set by a matrix a_j = (0.01, 0.015, 0.02, 0.025, 0.03, 0.035, 0.04, 0.045, 0.05, 0.055, 0.06). All educational information is divided into two categories: 1) knowledge and skills K_1 which are used daily and therefore are badly forgotten (reading, the letter, arithmetic actions, the simple facts, etc.); 2) knowledge K_2 which are applied seldom and therefore are quickly forgotten (difficult theories, principles, lows, facts). Levels of requirements the teachers corresponding to knowledge K_1 and K_2 which need to be acquired in j–th class, are set by matrixes: U_1 = (50, 46, 42, 36, 30, 25, 20, 15, 10, 10, 10) and U_2 = (4, 8, 14, 18, 24, 28, 33, 38, 46, 58, 62). Coefficients of forgetting of knowledge K_1 and K_2 are equal 0.002 and 0.01 consequently. It is necessary to calculate a total level of knowledge and amount of knowledge K_1 and K_2 at various moments t.
In this case knowledge K_1 and K_2 has different speed of forgetting, but don’t pass from one category into another. The offered two-component model of training is expressed by system of the equations:
Here U_1 and U_2 – levels of requirements the teachers corresponding to knowledge K_1 and K_2 which quantity is equal Z_1 and Z_2, and Z – total knowledge of the pupil. Computer program PR-1 is used.
Results of use of computer model are presented in fig. 2. On it are shows: 1) graphics Z_1(t) and Z_2(t) dependences of knowledge K_1 and K_2 from time; 2) the curve of dependence of total of knowledge Z from time; 3) graphics Z’_1(t) and Z’_2(t) dependences of knowledge K_1 and K_2 acquired by the pupil in the 10-th class from time. It is visible that during training in school the total amount of knowledge, and also quantity of knowledge K_1 and K_2 monotonously increase, and after training decrease due to forgetting. Knowledge K_1 is forgotten significantly quicker, than K_2. Values of the parameters are picked up so that the model corresponded to the typical situation meeting in student teaching.
Conclusions
In article is described the computer model of process of the training which is considering that: 1) durability of assimilation of various ELM isn’t identical, it is possible to allocate category of strong (durable) and weak knowledge; 2) strong knowledge is forgotten significantly more slowly than the weak; 3) weak knowledge at their use by the pupil gradually becomes strong. Also was modeled three situations, received the results which correspond to real process of training.
Offered computer models supplement qualitative reasoning, does them more objective, reasonable; they can be used when pedagogical experiment leads to negative results. If to change sequence of studying of various ELM, duration of lessons, etc., then possible to find an optimum way of training in a concrete case. Other direction of application of imitating modeling of process of learning consist in creation of the training computer program for simulating educational process at school which possible to use for training of students of pedagogical institutions.
References
- Dobrynina N.F. Matematicheskie modeli rasprostranenija znanij i upravlenija processom obuchenija studentov [Mathematical models of the spread of knowledge and learning management students]: Basic research, 2009, N 7.
- Dorrer A.G., Ivanilova T.N. Modelirovanie interaktivnogo adaptivnogo obuchajushhego kursa [Modeling of interactive adaptive course of learning: Modern problems of science and education], 2007, N 5 .
- Ivashkin Ju.A., Nazojkin E.A. Mul’tiagentnoe imitacionnoe modelirovanie processa nakoplenija znanij [Multi-agent simulation of the process of accumulation of knowledge]: Software products and systems, 2011, N 1, pp. 47 – 52.
- Kudrjavcev V.B., Vashik K., Strogalov A.S., Alisejchik P.A., Peretruhin V.V. Ob avtomatnom modelirovanii processa obuchenija [On the automaton model of the learning process]: Discrete Mathematics, 1996 , T. 8. , Vol. 4 , pp. 3 – 10.
- Leont’ev L.P., Gohman O.G. Problemy upravlenija uchebnym processom: Matematicheskie modeli [Problems Training Management: Mathematical model], Riga, 1984, 239 p.
- Mayer R.V. Issledovanie processa formirovanija jempiricheskih znanij po fizike [The study of the formation of empirical knowledge of physics], Glazov: GGPI, 1998. –– 132 p. Available at: http:// maier-rv.glazov.net .
- Mayer R.V. Osnovnaja zadacha matematicheskoj teorii obuchenija i ee reshenie metodom imitacionnogo modelirovanija [Main problem of mathematical theory of training its decision with using method of imitating modeling], Perspective of Science and Education, 2013, N 5, pp. 95–100.
- Solovov A.V., Men’shikov A.A. Diskretnye matematicheskie modeli v issledovanijah processov avtomatizirovannogo obuchenija [Discrete mathematical models in the study of processes automated training], Educational Technology & Society, 2001, N 4, pp. 205 – 210.
- Firstov V.E. Matematicheskie modeli upravlenija didakticheskimi processami pri obuchenii matematike v srednej shkole na osnove kiberneticheskogo podhoda [Mathematical models of control didactic process of teaching mathematics in secondary schools on the basis of the cybernetic approach]: diss. … doc. of pedagogical sciences. –– St. Petersburg, 2011, 460 p.

 View this article in Russian
View this article in Russian