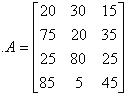Появление теории игр было обусловлено необходимостью анализировать проблемные ситуации в экономике, основываясь на математические методы. Спектр же применения этой области математического анализа довольно велик: в военном деле теория игр позволяет учесть в стратегии возможные действия противника, в бизнесе разрабатываемые модели используются для предвидения поведения конкурентов на изменение цен, формирование новых компании поддержки сбыта, производства новой продукции и т.д. Так например, если модели теории игр определяют, что при повышении цены на выпускаемую продукцию одной фирмой, остальные фирмы-конкуренты не сделают того же, то, вероятно, руководство откажется от этого управленческого решения, дабы не оказаться в невыгодном положении в конкурентной борьбе.
Конечно же, структура современного мира очень сложна и ситуации в нем меняются порой очень быстро, но полезность теория игр заключается в определении наиболее важных факторов, влияющих на принятие решений в условиях конкурентной борьбы. Поэтому теория игр в настоящее время рассматривается как один из эффективных методов разработки управленческих решений.
Вообще теория игр позволяет рассматривать самые различные ситуации: от шахмат до контроля над вооружением, поскольку представляет собой строгое стратегическое мышление, т.е. искусство предугадывать следующий ход соперника с учетом того, что он занимается тем же самым.
Рассмотрим некоторые прикладные аспекты теории игр.
Пусть требуется выбрать оптимальную стратегию, используя критерии Гурвица (α =0,4), Лапласа, Сэвиджа, Вальда.
Критерий Гурвица, α=0,4
Критерий Лапласа
Основывается на принципе недостаточного обоснования
Критерий Сэвиджа
Критерий Вальда
Для принятия стратегического решения составим управленческую таблицу:
Таблица 1. Управленческая таблица
| А – матрица выигрышей | А – матрица потерь | |
| критерий Гурвица (α =0,4), | 3 стратегия | 1 стратегия |
| критерий Лапласа | 4 стратегия | 1 стратегия |
| критерий Сэвиджа | 2 и3 стратегия | 1 стратегия |
| критерий Вальда | 3 стратегия | 1 стратегия |
Таким образом, если рассматриваемая матрица являлась матрицей выигрышей, то оптимальной стратегией является третья стратегия, если же рассматриваемая матрица являлась матрицей потерь, то оптимальной стратегией является первая стратегия.
Библиографический список
- Орехов Н.А., Левин А.Г., Горбунов Е.А. Математические методы и модели в экономике. Учебное пособие для вузов / Под ред. проф. Н.А. Орехова – М.: ЮНИТИ-ДАНА, 2004. – 398 с.
- Экономико-математические методы и прикладные модели: Учеб. пособие для вузов/ В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. — М.: ЮНИТИ, 2009. – 391 с.
- Экономико-математическое моделирование. Учебник для вузов / Под общ. ред. И.Н. Дрогобыцкого. – М.: Изд. «Экзамен», 2004. – 368 с.
- Шилова Н.А., Зеленина Л.И. Применение теории игр для моделирования популяции морских макроводорослей // Теоретические и прикладные аспекты математики, информатики и обоазования: материалы Междунарной научной конференции (Архангельск 16-21 ноября2014 г.) / редкол.: И.И. Василишин и др.; Сев. (Фрктич.) фудер. Ун-т им. М.В. Ломоносова; Ин-т мат. и информ. Болгар. акад. наук; Ин-т информатизации образования РАО; Моск. пед. гос. ун-т. , ISBN 978-5-261-00990-0 – Архангельск: САФУ, 2014. – С.149 – С.155