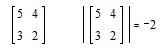Одной из основных задач методики преподавания любой дисциплины является повышение эффективности обучения и, как следствие, – лучшая подготовка студентов по тому или иному предмету. Достичь усиления эффективности обучения можно разными путями. В данной статье рассматривается использование межпредметных связей в курсе информатики по направлению 040700.62 «Организация работы с молодёжью» как способ повышении уровня практической и научно-теоретической подготовки студентов.
Существует много различных определений понятия «межпредметные связи» и несколько их классификаций. В Российской педагогической энциклопедии даётся следующее определение этого понятия: «Межпредметные связи – это комплексный подход к воспитанию и обучению, позволяющий вычленить как главные элементы содержания образования, так и взаимосвязи между учебными предметами» [1, т.2, с.563.].
Наиболее часто, рассматривая межпредметные связи с позиций целостности процесса обучения, производят следующую их классификацию: 1) содержательно-информационные; 2) фактические; 3) теоретические и 4) понятийные.
В данной статье межпредметные связи будут рассмотрены, прежде всего, как фактические, а точнее, как возможности применения методов информатики для разностороннего изучения объектов математики. Использование информационных технологий для математических вычислений и исследований, с одной стороны, закрепляет математические знания студентов, а с другой стороны, демонстрирует преимущества компьютерных программ, ускоряющих вычисления и облегчающих построение геометрических объектов.
Однако, для того, чтобы применение информационных технологий не было формальным, студенты должны освоить все алгоритмы вычислений и построений теоретически, «на бумаге», и лишь потом, понимая какие алгоритмы заложены в компьютерные программы, использовать эти программы как инструменты вычислений.
Приведём несколько конкретных примеров.
Занятие № 1. Тема: «Построение графиков функций».
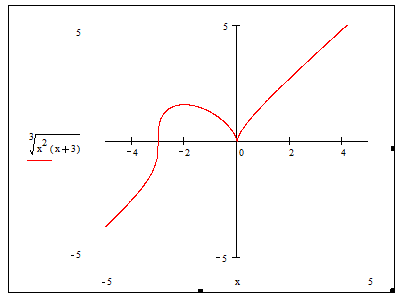
Задание. Постройте график функции ![]() Предлагаем студентам выполнить это задание тремя способами:
Предлагаем студентам выполнить это задание тремя способами:
- Письменно в тетради.
- В программе Excel.
- В программе MathCad.
Способ I.
Студенты исследуют функцию по известной схеме: находят ОДЗ, вычисляют производную, определяют промежутки возрастания и убывания функции, находят точки экстремума, максимума и минимума, а также точки перегиба и строят график функции.
Способ II.
Предлагается построить график этой же функции в программе Excel. Для этого студенты должны выполнить следующие действия:
- Определить функцию f (x) на отрезке от -5 до 5.
- Чтобы это сделать, в ячейки А1:А21 ввести значение аргумента при помощи автозаполнения, в данном случае, с шагом 0,5 (смотри рисунок).
- В ячейку В1 ввести значение функции, вычисляемое по формуле =(A1^2*(A1+3))^(1/3) (смотри рисунок).
- Ячейки В2:В21 заполняются копированием формулы (протаскиванием за маркер) из ячейки В1.
- Выделить диапазон А1:В21 и воспользоваться вкладкой Вставка, Точечная. Для построения графика функции лучше выбрать Точечную диаграмму с прямыми отрезками.

Чтобы график получился выразительным, можно уменьшить промежуток изменения аргумента, увеличить толщину линий, выделить оси координат, нанести на них соответствующие деления, сделать подписи на осях и ввести заголовок. Для этого:
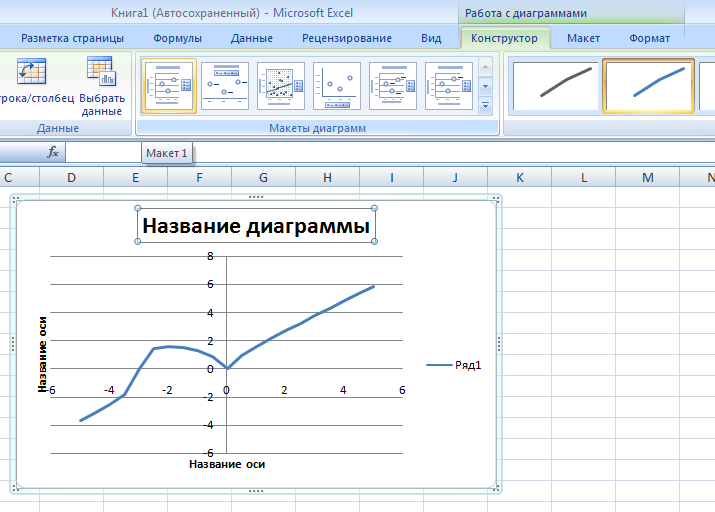
- Активизировать двойным щелчком график, на вкладке Работа с диаграммами перейти в Конструктор и выбрать Макет 1.
- Ввести название диаграммы и осей.
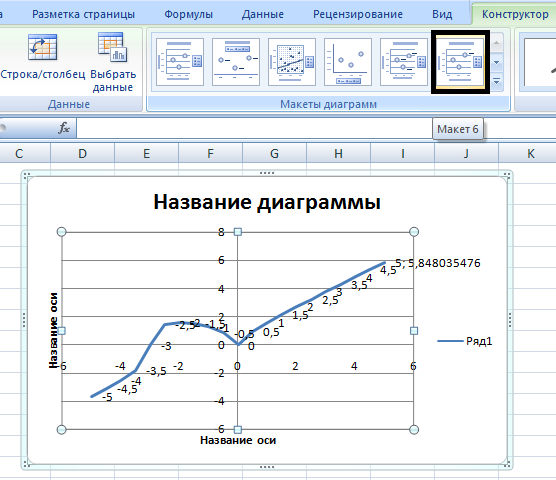
- Меняя макеты на Макет 3 и Макет 6, изменить вид графика. Оставить тот, что наиболее нагляден.
Способ III.
Предлагается построить график этой же функции в декартовой системе координат в программе MathCad. Для этого студенты должны выполнить следующие действия:
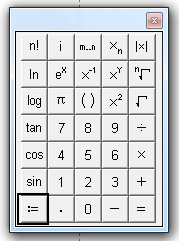
- Ввести формулу, пользуясь кнопкой Арифметические инструменты на панели Математика.
- Вместо знака «равно» (=) при задании функции используется знак «присвоить» (:=).
- Воспользоваться кнопкой Инструменты графиков панели Математика.
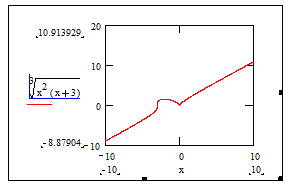
- Нажать кнопку Декартов график и в открывшемся окне ввести в маркер возле оси абсцисс имя аргумента (x), а в маркер возле оси ординат ввести или скопировать символьное значение функции (правую часть равенства).
- Щёлкнуть вне окна графиков. Получим график:
- Для изображения осей сделать двойной щелчок по графику:
Формат, Оси, Стиль осей, Пересечение.
- В англоязычной версии: в открывшемся окне поставить галочку возле слова Crossed.
- Изменить интервалы отображения на осях: по оси абсцисс – от -5 до 5, по оси ординат – от -5 до 5 для большей наглядности.
Итак, задание выполнено студентами тремя способами. Они могут сравнить полученные результаты и сделать выводы о преимуществах и недостатках каждого способа действий.
Занятие № 2. Тема: «Вычисление определителей матриц».
Рассмотрим все три способа действий на простейшем примере.
Задание. Дана матрица ![]() Вычислить её определитель.
Вычислить её определитель.
Способ I.
Письменно находим определитель:
Решим эту задачу в Excel. Для этого студенты должны выполнить следующие действия:
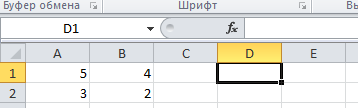
- Ввести числа в соответствующие ячейки, например в А1:В2:
- Активизировать ячейку D1. В ней будет результат вычисления.
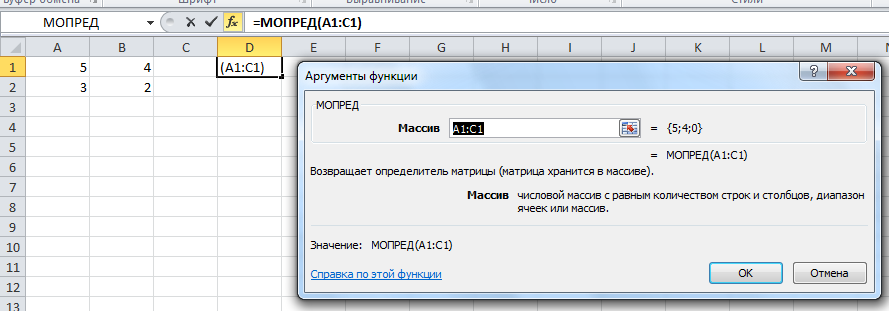
- В мастере функций выбрать функцию МОПРЕД (сокращение от Матрица, ОПРЕДелитель).
- В окне Аргументы функции в поле массив ввести данные, выделив их прямо на листе Excel:
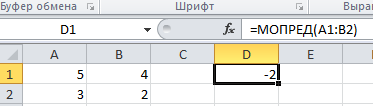
- В ячейке D1 будет получен результат:
Способ III.
Проведём вычисление этого же определителя в программе MathCad.
- На панели Математика выбрать кнопку Матрицы, и на появившейся панели – аналогичную кнопку.
- В открывшемся окне выставить количество строк и столбцов матрицы.
- Ввести числа.
- Нажать кнопку Определитель (Determinant).
- Выделить матрицу, скопировать и вставить в окошко определителя.
- Переместить курсор в конец формулы и нажать Равно (или на клавиатуре, или на панели Арифметические инструменты ).
- Будет получен результат:
Студенты убеждаются, что результаты, найденные разными способами – совпадают.
Аналогичную работу можно провести и по другим темам курса математики, показывая студентам, как компьютерные программы помогают человеку в сложных и трудоёмких вычислениях. Однако студенты должны понимать суть производимых машиной вычислений, анализировать полученные с помощью компьютера результаты. Поэтому в первую очередь необходима теоретическая подготовка по математике. Лишь после освоения студентами алгоритмов вычислений, можно «доверить» эти вычисления компьютеру.
Библиографический список
- Российская педагогическая энциклопедия: в 2 т. М.: Изд. Большая Российская энциклопедия, 1999. Т 2, 860 с.
- М.С. Мирзоев. Содержание и компоненты математической культуры бакалавров-педагогов профиля «Информатика» в условиях интеграции предметных областей «Математика» и «Информатика»: Журнал «Наука и школа», № 2, 2015