В курсе информатики старшей школы особое место занимает тема «Игры и стратегии». Она появилась относительно недавно, но является эффективным компонентом информационного моделирования. Изучение данной темы возможно и необходимо в базовом курсе информатики.
Как известно игра многофункциональна. В детстве в игре приобретаются новые и уточняются уже имеющиеся знания, активизируется любознательность, пытливость, развиваются нравственные качества: воля, смелость, выдержка. Во взрослой жизни создаются модели взаимодействий, позволяющие проигрывать разные ситуации в процедурах принятия решений. В игровой модели участники выполняют различные роли: партнеров-соперников, начальников и подчиненных, продавцов и покупателей, заказчиков и подрядчиков.
Игры различают по объему информации, имеющейся у игроков относительно прошлых партий и ходов: игры с полной и неполной информацией.
В школьном курсе информатики рассматриваются игры с полной информацией, которые требуют для их решения построения дерева игры. Вариантов построения дерева множество. Это и схема, и таблица, и, в конце концов, словесное описание.[1]
Однако, на мой взгляд, представляется наиболее эффективным для решения данных задач использовать организационные диаграммы.
Как известно, организационные диаграммы используют для графического описания иерархических отношений. Диаграмма формируется добавлением и/или удалением фигур, изменением их расположения, а также добавлением текста к фигурам диаграммы.
Макет организационной диаграммы по умолчанию содержит четыре фигуры. Для добавления фигуры необходимо выделить фигуру диаграммы, к которой добавляется новая, и в появившемся меню выбрать тип добавляемого элемента (Подчиненный, Коллега, Помощник).
Построение полного дерева игры – это рассмотрение для каждой позиции игры всех возможных ходов. Затем для получившихся позиций – снова рассмотрение всех возможных ходов. И так до тех пор, пока по всем получившимся “направлениям” мы не достигнем конца игры.
Рассмотрим пример задачи:
Перед игроками лежат две кучки камней по 4 камня. За один ход разрешается увеличить число камней в любой из кучек в 3 раза или добавить в кучку 1 камень. Выигрывает тот, кто получает суммарное количество камней больше 20 [2]
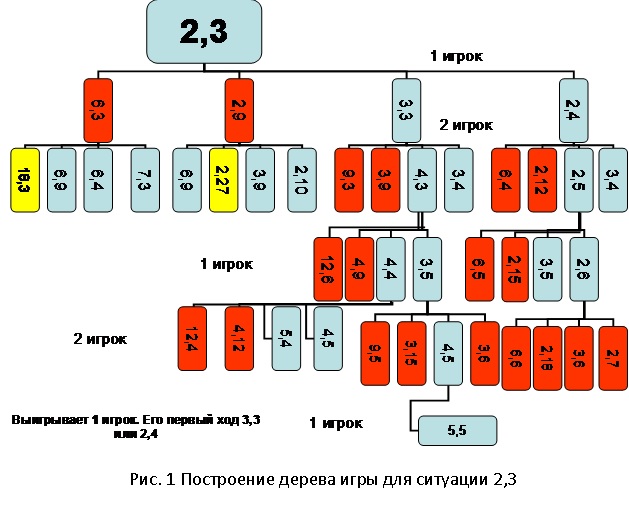
Для изображения дерева игры используем организационную диаграмму (рис.1).
А вот так будет выглядеть дерево игры в ситуации, когда количество камней в кучках будет 2 и 3.
Организационная диаграмма позволяет четко разграничить возможные ходы игроков. Она дает возможность увидеть как проигрышные, так и выигрышные комбинации. Наглядность организационной диаграммы позволяет сделать правильный вывод о победителе игры практически всем учащимся. В этом, безусловно, главное преимущество такого способа решения задачи. Следует не забывать также, что использование организационной диаграммы позволяет отрабатывать и технологические навыки их построения в различных офисных приложениях, что тоже немаловажно для будущих выпускников школ.
В реальной жизни практически постоянно приходится сталкиваться с ситуациями, в которых необходимо принимать решения в условиях неопределенности, т. е. возникают ситуации, в которых две (или более) стороны преследуют различные цели, а результаты любого действия каждой из сторон зависят от мероприятий партнера. В этом смысле изучение теории игр в базовом курсе информатики является реализацией требований Федеральных государственных образовательных стандартов по формированию у учащихся универсальных учебных действий, достижению личностных результатов.
Библиографический список
- К.Ю. Поляков. ЕГЭ по информатике 2016. URL: http://kpolyakov.spb.ru/download/ege26-C3.doc
- Гейн А.Г. и др.Информатика и ИКТ. 11 класс. Базовый и профильный уровни. М.: 2009.