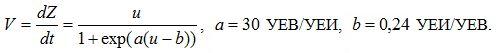Проблема понимания или непонимания учеником сообщаемого ему учебного материала имеет большое практическое значение [8], поэтому ее изучением занимались многие ученые. Например, Е.Т. Коробов в своей статье [1] анализирует понимание с дидактической точки зрения и выделяет психологические, дидактические, лингвистические, логические, физиологические причины непонимания. Хорошо известно, что уровень понимания сообщаемой информации зависит от скорости ее поступления. Если скорость сообщения учебного материала больше некоторого порогового значения, то ученик перестает понимать учителя. В настоящей статье предпринята попытка изучения зависимости скорости понимания новой информации от скорости ее сообщения методами имитационного моделирования на компьютере [9].
Сущность метода имитационного моделирования состоит в построении компьютерной модели исследуемой системы и проведении серии вычислительных экспериментов с целью понимания поведения системы или оценки различных стратегий управления, обеспечивающих ее функционирование. В настоящее время методы математического и компьютерного моделирования широко используются при изучении дидактических систем [3–7]. Особый интерес представляет собой обезразмеренное моделирование, при котором объем сообщаемой информации, количество знаний ученика и время могут измеряются в условных единицах УЕИ и УЕВ [4]. Это позволяет проанализировать закономерности дидактического процесса в самом общем виде.
Учебный материал дискретен, он состоит из отдельных теоретических блоков, которые в свою очередь делятся на элементы учебного материала (ЭУМ): понятия, формулы, утверждения, иностранные слова, логические переходы и т.д. Обучение аналогично просмотру учебного фильма, в ходе которого на экране последовательно сменяются блоки информации (предложения, рисунки, формулы). Ученик понимает новый блок сообщаемой информации в том случае, если он понимает каждый входящий в него ЭУМ. Если ученик не усвоил какой–либо ЭУМ в блоке, то он не усваивает блок в целом (то есть не может решить задачу, доказать теорему, правильно перевести предложение). Понимание каждого ЭУМ происходит с некоторой вероятностью p.
Основная идея компьютерного моделирования понимания учебного материала состоит в следующем. Если в блоке m ЭУМ, то на усвоение одного блока у ученика имеется время t1 = m / u, где u – скорость сообщения информации учителем. Когда ученик понимает все m (например, 4) ЭУМ, он понимает весь блок, поднимается флаг (flag:=1) и переменная Pon_bl увеличивается на 1. Вероятность понимания одного ЭУМ c первого раза равна p (например, p = 0,8). Если ученик не понял ЭУМ с первого раза, то он обращается к нему снова до тех пор, пока не поймет, либо пока не закончится время t1, отводимое на понимание данного блока, и от учителя не придет следующий блок информации. Пусть все ЭУМ имеют одинаковый информационный объем равный 1 условной единице информации. Время однократного обращения ученика к ЭУМ t_obr = 1/vm, где vm – скорость его мыслительной деятельности: чем больше мыслительных действий совершает ученик в единицу времени, тем выше его способность понять данный ЭУМ.
Программа 1, позволяющая изучить зависимость усвоения от скорости поступления информация, состоит из цикла по времени, которое изменяется с шагом 0,01. Перед усвоением блока переменные EUM и flag обнуляются, счетчик блоков N_bl увеличивается на 1 и вычисляется время, отводимое на усвоение одного блока t1. Количество m ЭУМ в блоке задается так: с вероятностью 0,3 число m равно 4, с вероятностью 0,3 число m равно 6, с вероятностью 0,4 число m равно 5. Когда время работы ученика с одним ЭУМ k*dt превышает значение t_obr, программа моделирует случайный процесс понимания ЭУМ с вероятностью p. Если случайное x из интервала [0; 1] меньше p, то считается, что ученик понял ЭУМ и переменная EUM увеличивается на 1. Если при этом переменная EUM=m, то ученик понял весь блок из m ЭУМ; Pon_bl увеличивается на 1, флаг поднимается (flag=1). Если ученик не успевает понять все m ЭУМ за время t1, то считается, что он не понял данный блок. После этого ученик “изучает” второй блок информации и т.д. Так повторяется до тех пор пока число сообщенных блоков N_bl не достигнет 2000.
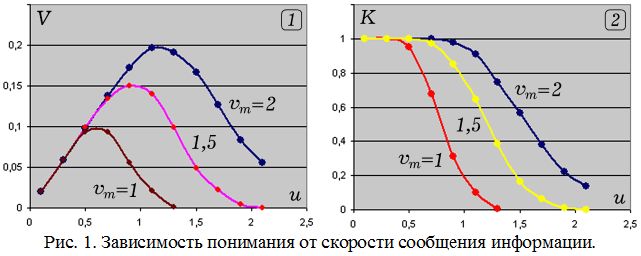
Программа выводит на экран количество сообщенных блоков N_bl, число понятых блоков Pon_bl и затраченное время t, что позволяет определить скорости сообщения информации u = N_bl / t и скорость усвоения V = Pon_bl / t (в блок/УЕВ). На рис. 1.1 представлены графики зависимости скорости усвоения V от скорости сообщения информации учителем u (блок/УЕВ) при различных значениях скорости мышления ученика vm. Видно, что при небольшой скорости сообщения информации учителем скорость усвоения V = u (тоже растет), так как ученик с данной скоростью совершения мыслительных операций успевает понять практически все сообщаемые учителем блоки. Дальнейшее возрастание скорости сообщения информации u приводит к тому, что ученик не успевает воспринять ее полностью: скорости усвоения V достигает максимума, а затем снижается. Чем больше скорость мыслительных действий ученика vm, тем больше максимально возможная скорость усвоения V и соответствующая ей скорость сообщения информации учителем u. В книге Л.П. Леонтьева и О.Г. Гохмана [2, с. 108–157] рассмотрены различные математические модели, связывающие объем усвоенного информации с объемом изложенного на лекции материала. Соответствующие им графики очень похожи на кривые, изображенные на рис. 1.1.
Введем коэффициент понимания материала K, как отношение количества понятых блоков к общему количеству сообщенной информации. При малых скоростях передачи информации u ученик понимает практически все, что сообщает учитель, поэтому K = 1. По мере увеличения u коэффициент понимания K плавно уменьшается до 0. При увеличении скорости мыслительных действий vm скорость сообщения информации u учителем, соответствующая K = 0,5 увеличивается (рис. 2).
Используя электронные таблицы Excel, можно достаточно точно подобрать функцию, соответствующую получившимся графикам. Для vm = 1,5 она имеет вид:
Если u < 0,9b, то знаменатель примерно равен 1, скорость увеличения знаний ученика V равна скорости сообщения знаний учителем u. Когда u превышает b, знаменатель дроби начинает увеличиваться сначала медленно, а потом все быстрее. При u>4b скорость V уменьшается, стремясь к 0. По мере обучения ученика увеличивается его скорость мышления vm, повышается способность быстро усваивать учебный материал. Скоростям vm = 1, 1,5, 2 соответствуют следующие значения параметров: a = 38, b = 0,16; a = 30, b = 0,235; a = 20, b = 0,315.
Получившиеся графики можно интерпретировать иначе. Допустим ученик решает задачи, каждая из которых требует выполнения m сложных операций. Вероятность правильного выполнения каждой сложной операции равна p. Если ученик не выполнил операцию с первого раза, то он делает вторую попытку и т.д. На одну задачу отводится фиксированное время t1 = m/u. На каждую попытку выполнить операцию ученик затрачивает время t_obr = 1/vm. График K = K(u) на рис. 1.2 показывает зависимость вероятности решения задач от скорости их поступления u (которая обратно пропорциональна t1), при различных скоростях мышления vm. По оси абсцисс также может быть отложена сложность задач.
Таким образом, в настоящей статье предложена компьютерная модель понимания учебного материала, в основе которой лежат следующие утверждения: 1) информация состоит из блоков, в каждом из которых 4-6 элементов учебного материала; 2) все элементы учебного материала имеют одинаковую сложность, поэтому ученик понимает их с одинаковой вероятностью; 3) время обращения ученика к данному элементу учебного материала обратно пропорционально его скорости мышления. Полученные графики зависимости скорости понимания и коэффициента усвоения от скорости изложения учебного материала соответствуют основным положениям психологии.
Библиографический список
- Коробов Е.Т. Понимание как дидактическая проблема // Московский психологический журнал. – 2005. – № 11. URL: http://magazine.mospsy.ru/nomer11/s10.shtml
- Леонтьев Л. П., Гохман О. Г. Проблемы управления учебным процессом: математические модели. – Рига, 1984. – 239 с.
- Майер Р. В. Имитационное моделирование изучения студентами вузовского курса, учитывающее психологические закономерности усвоения и забывания // Концепт. – 2015. – № 12 (декабрь). – ART 15430. – URL: http://e-koncept.ru/2015/15430.htm. – ISSN 2304-120X.
- Майер Р.В. Кибернетическая педагогика: Имитационное моделирование процесса обучения: монография. – Глазов: Глазов. гос. пед. ин–т, 2014. – 141 с. URL: http://maier-rv.glazov.net
- Майер Р.В. Результаты имитационного моделирования обучения в 11–летней школе // Современные научные исследования и инновации. 2015. № 11 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/11/59115 (дата обращения: 12.11.2015).
- Робертс Ф.С. Дискретные математические модели с приложениями к социальным, биологическим и экологическим задачам. – М.: Наука, Гл. ред. физ. –мат. лит., 1986. – 496 с.
- Титов Б.А., Рябинова Е.Н. Математическая модель усвоения учебной информации в образовательном процессе // Вестник Самарского государственного аэрокосмического университета N 3 (27), 2011, С. 334–340.
- Фридман Л.М., Кулагина И.Ю. Психологический справочник учителя. – М.: Просвещение, 1991. – 288 с.
- Шеннон Р. Имитационное моделирование систем: искусство и наука. – М.: Мир, 1978. – 302 с.