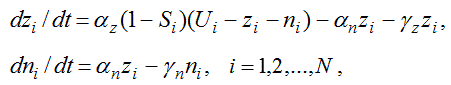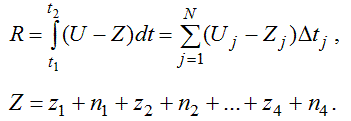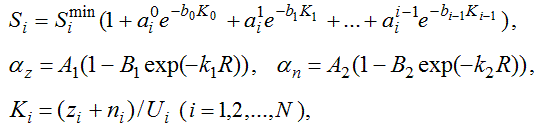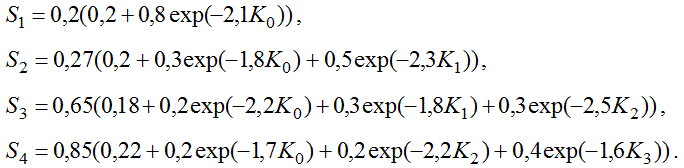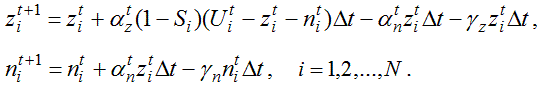Введение

Допустим, имеется группа из n учеников, каждый из которых характеризуется определенными коэффициентами усвоения и забывания. Их обучает учитель, владеющий определенным набором методов, которые, в соответствии с учебной программой, должны обеспечить усвоение некоторого учебного курса. Основная задача математической теории обучения может быть сформулирована так: зная параметры учащихся, характеристики используемых методов и учебную программу (распределение учебной информации), используя математическую модель обучения, необходимо определить уровень знаний (или сформированности навыка) у учащихся во время прохождения курса и после его окончания.

Понятно, что развитие теории обучения предполагает создание различных математических моделей ученика и учителя и их использование для решения частных задач, сводящихся к анализу конкретных ситуаций, возникающих при обучении. Для этого используются метод математического моделирования [1,2,6] и метод компьютерного (имитационного) моделирования [3–5]. Сила математической теории обучения состоит в точном и полном указании всех условий и факторов, влияющих на анализируемую ситуацию, возникающую в процессе обучения. При этом должны быть однозначно определены: 1) используемая математическая модель (система уравнений); 2) параметры ученика (коэффициенты усвоения, забывания и т.д.); 3) порядок поступления элементов учебного материала (ЭУМ); 4) сложность изучаемых ЭУМ, и ее зависимость от уровня усвоения ранее изученных ЭУМ.

Как следует из [3 – 5], компьютерные модели процесса обучения дополняют качественные рассуждения, делают их более объективными, обоснованными и могут быть использованы тогда, когда проведение педагогического эксперимента требует больших затрат, неправомерно или приводит к отрицательным результатам. Изменяя последовательность изучения различных ЭУМ, длительность занятий и параметры ученика, можно с помощью компьютерной модели исследовать влияние тех или иных факторов на результат, найти оптимальный путь обучения в конкретном случае.

1. Непрерывная двухкомпонентная модель “знания-навыки”

Рассмотрим двухкомпонентную модель ученика, изучающего некоторую дисциплину, состоящую из N тем. Будем считать, что уровень знаний Z_i учеником i–той темы складывается из двух составляющих: 1) знаний первой категории z_i (или непрочных знаний), которые быстро забываются; 2) знаний второй категории n_i (прочных знаний или навыков), которые забываются существенно медленнее. Получаем следующую систему уравнений:

где U_i – уровень требований учителя при изучении i-той темы, который равен количеству ЭУМ, которые должен усвоить ученик, S_i – сложность i-той темы, a_z и a_n, g_z и g_n –– коэффициенты усвоения и забывания для непрочных и прочных знаний. В общем случае сложность изучения i–ой темы зависит от коэффициентов изученности предыдущих тем: S_i=S_i(K_j) (j = 0, 1, 2, …, i-1), а коэффициенты усвоения a_z и a_n –– от суммарных усилий, приложенных учеником R, и от количества усвоенных знаний: a_z=f(R, Z), a_n=f(R,Z). При этом:

Сложность i–ой темы и коэффициенты усвоения можно задать уравнениями:

где K_i – коэффициенты изученности i–ой темы, показывающие какая часть учебной информации усвоена, а K_0 – коэффициент изученности предыдущего учебного материала. Коэффициенты b_i должны быть подобраны так, чтобы при K_i стремящимся к 1 сложность изучения i–той темы приближалась бы к своему минимальному значению. При увеличении затраченных усилий (или совершенной работы) R коэффициенты усвоения a_z и a_n стремятся к A_1 и A_2.

2. Компьютерная программа, моделирующая обучение

Проанализируем использование предложенной модели для анализа следующей ситуации: Ученик изучает курс, состоящий из 4 тем, сложности которых задаются уравнениями:

Здесь K_i – коэффициенты изученности i–той темы (i = 1, 2, 3, 4). Длительности изучения тем соответственно равны: T_1=70 УЕВ (усл. ед. времени), T_2=93 УЕВ, T_3=104 УЕВ, T_4=135 УЕВ. Уровень требований учителя при изучении каждой  i–ой темы возрастает по линейному закону от 0 до максимального значения U_m со скоростью U_m/T. В нашем случае максимальные значения U_m для 1, 2, 3, 4 тем соответственно равны 52, 90, 105, 116. Будем считать, что коэффициенты усвоения ученика зависит от выполненной им работы следующим образом:

где R_i (I = 1, 2, 3, 4) – усилия, затраченные учеником при освоении i–ой темы. Коэффициенты забывания g_z=0,005, g_n=0,0002.

                                                                                                                                                                                                                     Программа ПР–1.

Пусть после прохождения курса в заданный момент времени t’=400 УЕВ ученик выполняет тест по каждой теме, состоящий из 10 заданий возрастающей сложности C_j. Вероятность правильного выполнения j-ого задания теста по i–ой теме определяется формулой Роша:

где b=0,02. Необходимо изучить зависимость количества знаний ученика с течением времени и определить результаты тестирования по каждой теме.

Используемая компьютерная программа, содержит цикл по времени, в котором для каждого момента t вычисляются коэффициенты усвоения a_z и a_n, сложность S_i изучаемой темы, уровни знаний z_i и навыков n_i ученика по каждой теме, совершенная им работа R_i (i=1, 2, 3, 4), а результаты выводятся на экран. При этом применяются следующие конечно–разностные уравнения:

В статье приведен упрощенный вариант компьютерной программы (ПР–1), которая моделирует изучение двух тем. Для компьютерной симуляции рассмотренной выше ситуации с курсом из 4 тем применяется аналогичная программа.

3. Результаты моделирования и их анализ

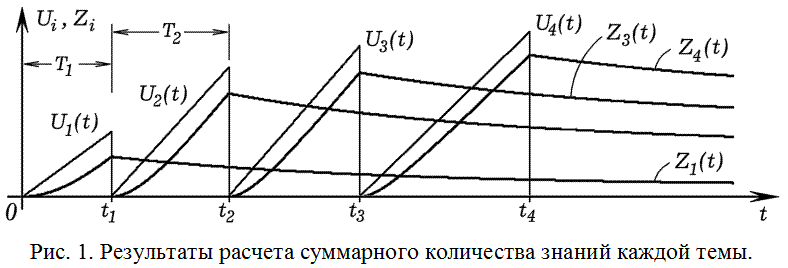
Использование рассмотренной выше модели дает результаты представленные на рис. 1, 2, 3. На рис. 1 изображены графики зависимости уровня требований U_i(t) учителя и количества знаний Z_i(t) учеников от времени для 1, 2, 3 и 4 тем. Видно, что при изучении i–ой темы количество U_i сообщаемых учителем знаний, которые должны усвоить ученики, растет пропорционально времени. Количество знаний ученика Z_i=z_i+n_i возрастает, а после окончания изучения темы убывает вследствие забывания непрочных знаний.

На рис. 2 представлены графики зависимостей от времени суммарного количества знаний по всем темам Z(t), общего количества прочных знаний (навыков) N(t)=n_1+n_2+n_3+n_4, совершенной учеником работы R(t) и коэффициента усвоения a_z. Видно, что во время обучения (t<t_4) происходит следующее: 1) суммарное количество знаний Z ученика растет; 2) количество прочных знаний N также возрастает, но несколько медленнее; 3) растет суммарное количество затраченных усилий R, что приводит к повышению коэффициента усвоения a_z. После окончания обучения (t>t_4): 1) количество знаний Z уменьшается из–за быстрого забывания непрочных знаний первой категории; 2) количество прочных знаний N уменьшается с существенно меньшей скоростью; 3) коэффициент усвоения a_z остается неизменным.

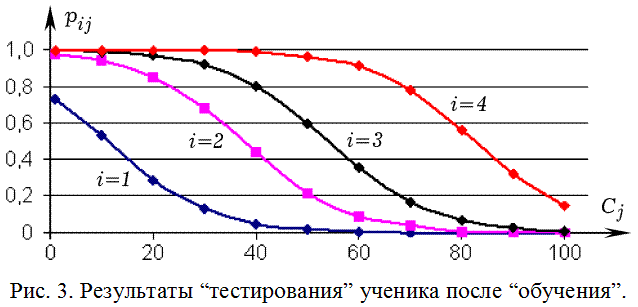
Результаты “выполнения” учеником 40 заданий теста (по 10 заданий на каждую тему) представлены на рис. 3.  По оси абсцисс отложена сложность заданий C_j, а по оси ординат – вероятность p_ij правильного выполнения j–того задания по теме i. Из графиков видно, что: 1) ученик хорошо справляется с простыми заданиями, и гораздо хуже со сложными; 2) из–за забывания результаты тестирования по первой и второй темам существенно ниже, чем по третьей и четвертой темам.

Заключение

Предложена многокомпонентная компьютерная модель обучения, основанная на том, что: 1) прочность усвоения различных ЭУМ неодинакова; 2) прочные знания забываются существенно медленнее непрочных; 3) непрочные знания при их использовании учащимся постепенно становятся прочными. Она позволяет промоделировать процесс обучения, учитывая что: 1) курс состоит из нескольких тем; 2) сложность каждой темы зависит от уровня изученности учеником предыдущих тем; 3) при выполнении учащимся учебных заданий увеличивается его коэффициент усвоения, характеризующий способность усваивать новую информацию. Эта модель не имеет аналогов в известной автору литературе. Результаты моделирования хорошо согласуются с основными выводами теории обучения.

1. Добрынина Н.Ф. Математические модели распространения знаний и управления процессом обучения студентов. – Фундаментальные исследования. – 2009. – N 7. – с. 7 – 9.
2. Леонтьев Л.П., Гохман О.Г. Проблемы управления учебным процессом: Математические модели. – Рига, 1984. – 239 с.
3. Майер Р.В. Компьютерная модель обучения с изменяющимся коэффициентом забывания – International Journal of Open Information Technologies – Vol 2, No 1 (2014). – pp. 12–16. (http://injoit.org/index.php/j1)
4. Майер Р.В. Кибернетическая педагогика: Имитационное моделирование процесса обучения. – Глазов, ГГПИ, 2014. – 140 c. (http://maier-rv.glazov.net)
5. Майер Р.В. Многокомпонентная модель обучения и ее использование для исследования дидактических систем // Фундаментальные исследования: Педагогические науки. – 2013. – N 10. – С. 2524 –– 2528.
6. Фирстов В.Е. Математические модели управления дидактическими процессами при обучении математике в средней школе на основе кибернетического подхода: Дисс. … докт. пед. наук. – С. Петербург., 2011. – 460 с.

Все статьи автора «Майер Роберт Валерьевич»