ОЛИМПИАДА – ВЕРШИНА ЗНАНИЙ

Как говорил Исаак Ньютон «В математических вопросах нельзя пренебрегать даже с самыми мелкими ошибками». Поэтому в данном разделе мы разберем несколько олимпиадных задач из алгебры и геометрии, в которых можно быстрее сделать ошибку чем решить её.

Для начала одну из легких задач из неравенств алгебры

Задача №1: Докажите, что при любых положительных числах a и b

Доказательство: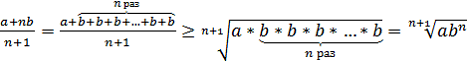 

Арифметическое и геометрическое среднее

Что и требовалось доказать.

Как мы видим сама по себе имела очень сложный структурный вид, но решение оказалось очень простым. Далее рассмотрим задачи из теории чисел и геометрии.

Задача №2: Найдите все такие простые числа p при котором соотношение

является квадратом целого числа.

Решение:

Так как p простое то,

Заметим что, НОД ()=1

Если  будет делиться на p то 

а это значит что  тогда a=2k+1 потому что оно должно быть нечетным

Подставляя получим 

Теперь рассмотрим еслибудет делиться на pтогда

 отсюда b должно быть нечетным, то есть

отсюда выходит следующее,а это возсоможно только при t=1 и k=2 подставляя находим что p=7

Ответ: 3 и 7

Задача №3: Точки P и Q — основания перпендикуляров, опущенных из вершины C на прямые, содержащие биссектрисы углов ∠BAC и ∠ABC соответственно. Докажите, что прямые AB и PQ — параллельны.

Доказательство: – Точка пересечения биссектрис , тогда четырёхугольник XQPC описанный , откуда углы ∠QPC=90∘−∠BAC2 и ∠PQC=90∘−∠ABC2 . Тогда если продлить PQ до пересечения со сторонами AC и BC , обозначим точки пересечения X И Y соответственно , то получим что ∠CPX=180∘−∠QPC−∠ABC=∠BAC , так же и с другим углом , проучим что PQ||AB .

Задача№4 Найдите все простые числа p, q и r, для которых выполняется равенство: p + q = (p – q)^r.

Решение: Из условия видно, что p + q делится на p – q, следовательно, (p + q) – (p – q) = 2q также делится на p – q. Делителями числа 2q могут являться только числа 1, 2, q и 2q.
Если p – q = 1, то левая часть исходного равенства больше правой. Если p – q равно q или 2q, то p равно 2q или 3q, то есть число р – не простое. Значит,
р – q = 2. Тогда исходное равенство примет вид: 2q + 2 = 2^r ⇔ q = 2^r–1 – 1. Если r = 2, то q = 1 – не простое число. Значит, r нечетно и r – 1 = 2k. Далее можно рассуждать по-разному.

Первый способ. 2^r–1 – 1 = 4^k – 1 делится на 4 – 1 = 3. Таким образом, q = 3. Тогда р = 5 и r = 3.

Второй способ. Так как q = 2^2k – 1 = (2^k – 1)(2^k + 1), то q может оказаться простым числом только в случае, когда 2^k – 1 = 1. Значит, k = 1, r = 3, q = 3, р = 5.

Ответ: p = 5, q = 3, r = 3.

Задача№5 Найти хотя бы одно целочисленное решение уравнения aІbІ + aІ + bІ + 1 = 2005.

Решение: (aІ + 1)(bІ + 1) = aІbІ + aІ + bІ + 1 = 2005 = 5·401 = 1·2005. Поскольку число 2004 не является полным квадратом, получаем 8 решений; все они получаются из (2, 20) перестановкой и сменой знаков.

Ответ: Например, a = 2, b = 20.

Задача№6 В трапеции ABCD углы при основании AD удовлетворяют неравенствам A < D < 90^o. Докажите, что тогда AC > BD.

Решение: Пусть B₁ и C₁ — проекции точек B и C на основание AD. Так как BAB₁ < CDC₁ и BB₁ = CC₁, то AB₁ > DC₁ и поэтому B₁D < AC₁. Следовательно, BD² = B₁D² + B₁B² <AC₁² + CC₁² = AC².

Задача №7 Даны n точек A₁,…, A_n и окружность радиуса 1. Докажите, что на окружности можно выбрать точку M так, что MA₁ + … + MA_n  n.

Решение: Пусть M₁ и M₂ — диаметрально противоположные точки окружности. Тогда M₁A_k + M₂A_k  M₁M₂ = 2. Складывая эти неравенства для k = 1,…, n, получаем (M₁A₁ + … +M₁A_n) + (M₂A₁ + … + M₂A_n)  2n. Поэтому либо M₁A₁ + … + M₁A_n  n, и тогда положим M = M₁, либо M₂A₁ + … + M₂A_n  n, и тогда положим M = M₂.

Все статьи автора «Iskander Tolebergen»